题目内容
4.某商家独家销售具有地方特色的某种商品,每件进价为40元,经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:| 销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润不低于8000元?
(3)在雅安地震发生时,商家已将商品一周的销售利润全部寄往灾区,已知商家购进该商品的货款不超过10000元,请你分析该商家当时最大捐款数额是多少元?
分析 (1)设y=kx+b,把点的坐标代入解析式,求出k、b的值,即可得出函数解析式;
(2)根据利润=(售价-进价)×销售量,列出函数关系式,继再利用销售利润为8000,进而得出销售单价的范围;
(3)根据购进该商品的贷款不超过10000元,求出进货量,然后求最大销售额即可.
解答 解:(1)设y=kx+b,
由题意得,$\left\{\begin{array}{l}{55k+b=450}\\{60k+b=400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-10}\\{b=1000}\end{array}\right.$,
则函数关系式为:y=-10x+1000,(x≥50)
故答案为:y=-10x+1000(x≥50);
(2)由题意得,S=(x-40)y=(x-40)(-10x+1000)
=-10x2+1400x-40000
=-10(x-70)2+9000,
当S=8000时,
8000=-10(x-70)2+9000,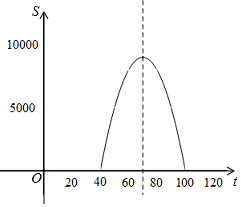
解得:x1=60,x2=80,
∵-10<0,
∴函数图象开口向下,对称轴为直线x=70,
∴当60<x<80时,销售利润一周的销售利润不低于8000元;
(3)∵由40(-10x+1000)≤10000
解得:x≥75,
又由于最大进货量为:y=10000÷40=250,
由题意可知,当x=75时,可以销售250件商品,结合图形,故此时利润最大.
S=250×(75-40)=8750(元),
故该商家在10000元内的进货条件下,最大捐款为8750元.
点评 本题考查了二次函数的应用,难度一般,解答本题的关键是将实际问题转化为求函数最值问题,从而来解决实际问题.

练习册系列答案
相关题目
19.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{30}$ | B. | $\sqrt{36}$ | C. | $\sqrt{40}$ | D. | $\sqrt{\frac{1}{7}}$ |
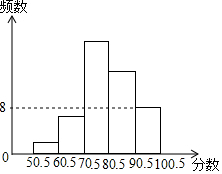 某班将全班同学一次知识竞赛成绩(整数)进行整理后,分成五组,绘成频数直方图,如图中从左到右的前四组的百分比分别是4%,12%,40%,28%,最后一组的频数是8,则该班有50名同学参赛.
某班将全班同学一次知识竞赛成绩(整数)进行整理后,分成五组,绘成频数直方图,如图中从左到右的前四组的百分比分别是4%,12%,40%,28%,最后一组的频数是8,则该班有50名同学参赛.