题目内容
2.某销售公司出示的楼价为:一楼每平方米14000元,每增高一层,每平方米楼价增加2000元(四楼以下).(1)写出每平方米楼价y元与楼层数x之间的关系式(四楼以下);
(2)如果从四楼开始至七楼每增高一层,每平方米楼价减少1800元,试写出每平方米楼价y元与楼层x之间的关系(4≤x≤7);
(3)请列出二至七楼每平方米的售价表,看看哪一层楼价最高和最低?
分析 (1)由每平方米楼价=一楼价格+(楼层数-1)×每增高一层多的钱数,即可得出每平方米楼价y元与楼层数x之间的关系式;
(2)先由(1)的结论算出3层房价,再结合每平方米楼价=三楼价格-(楼层数-1)×每增高一层少的钱数,即可列出每平方米楼价y元与楼层数x之间的关系式;
(3)由(1)(2)函数解析式即可得出二至七楼每平方米的售价,列出表格,根据表格数据即可得出结论.
解答 解:(1)根据题意可知:y=14000+2000(x-1)=2000x+12000.
故每平方米楼价y元与楼层数x之间的关系式为y=2000x+12000(1≤x≤3).
(2)令x=3,则y=2000×3+12000=18000,
根据题意可知:y=18000-1800(x-3)=-1800x+23400.
故每平方米楼价y元与楼层数x之间的关系式为y=-1800x+23400(4≤x≤7).
(3)根据(1)(2)即可列出售价表如下:
| XXX公司楼房售价表 | ||||||
| 楼层数(层) | 2 | 3 | 4 | 5 | 6 | 7 |
| 每平方米楼价 (元/平方米) | 16000 | 18000 | 16200 | 14400 | 12600 | 10800 |
点评 本题考查了一次函数的应用,解题的关键是:(1)(2)理清数量间的关系得出解析式;(3)通过(1)(2)结论得出数据填入表格.本题属于基础题,难度不大,解决该类题型读题是关键.

练习册系列答案
相关题目
10.M是线段AB的中点,P是MB上一点,PM等于( )
| A. | $\frac{1}{2}$(AM+PB) | B. | $\frac{1}{2}$(PA-PB) | C. | $\frac{1}{2}$AB-PB | D. | 以上都不对 |
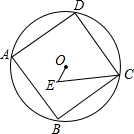 如图,正方形ABCD内接于⊙O,E是⊙O内的点,且∠E=60°,∠DCE=60°,若BC=6,则OE的长度是3-$\sqrt{3}$.
如图,正方形ABCD内接于⊙O,E是⊙O内的点,且∠E=60°,∠DCE=60°,若BC=6,则OE的长度是3-$\sqrt{3}$.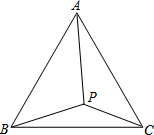 P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数?
P为等边△ABC内一点,且∠APC=110°,∠BPC=132°,试求以AP、BP、CP为边的三角形的度数? 如图,在边长为12$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于H,交AD于F点,连接CE,BH.若BH=16,则FG=10$\sqrt{2}$.
如图,在边长为12$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于H,交AD于F点,连接CE,BH.若BH=16,则FG=10$\sqrt{2}$.