题目内容
19.学校需要测量升旗杆的高度.同学们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.经测量,绳子多出的部分长度为2m,将绳子沿地面拉直,绳子底端距离旗杆底端6m,求旗杆的高度.分析 由题可知,旗杆,绳子与地面构成直角三角形,根据题中数据,用勾股定理即可解答.
解答 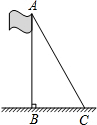 解:设旗杆的长度为xm,则绳子的长度为:(x+2)m,
解:设旗杆的长度为xm,则绳子的长度为:(x+2)m,
在Rt△ABC中,由勾股定理得:x2+62=(x+2)2,
解得:x=8,
答:旗杆的高度为8m.
点评 本题考查的是勾股定理的应用,根据题意得出直角三角形是解答此题的关键.

练习册系列答案
相关题目
9.已知等腰三角形的周长为20cm,底边长为y(cm),腰长为x(cm),y与x的函数关系式为y=20-2x,那么自变量x的取值范围是( )
| A. | x>0 | B. | 0<x<10 | C. | 0<x<5 | D. | 5<x<10 |
 如图,长方形ABCD中,AB=8,BC=10,将长方形沿折痕AF折叠,点D恰好落在BC边上的点E处.
如图,长方形ABCD中,AB=8,BC=10,将长方形沿折痕AF折叠,点D恰好落在BC边上的点E处.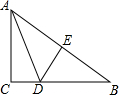 如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )
如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )