题目内容
7.先化简代数式:(1+$\frac{1}{x-2}$)÷$\frac{x^2-2x+1}{x^2-4}$,再从你喜欢的数中选择一个恰当的作为x的值,代入求出代数式的值.分析 先算括号里面的,再算除法,最后选取x的值代入进行计算即可.
解答 解:原式=$\frac{x-2+1}{x-2}$•$\frac{(x-2)(x+2)}{(x-1)^{2}}$
=$\frac{x+2}{x-1}$,
当x=0(x≠1,2,-2)时,原式=-2.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
18.若关于x的方程(k-1)x2-(k-1)x+$\frac{1}{4}$=0有两个相等的实数根,则k的值为( )
| A. | 1 | B. | 2 | C. | 1或2 | D. | 以上都不对 |
16.无论a取何值,下列各式中一定有意义的是( )
| A. | $\sqrt{a+1}$ | B. | $\sqrt{{a^2}-1}$ | C. | a-2 | D. | $\sqrt{{a^2}+1}$ |
 已知△ABC与△BDE都是正三角形,点A、B、E在同一直线上,求证:AD=CE.
已知△ABC与△BDE都是正三角形,点A、B、E在同一直线上,求证:AD=CE.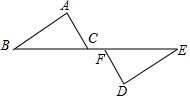 如图,△ABC≌△DEF,点B、F、C、E在同一条直线上.求证:
如图,△ABC≌△DEF,点B、F、C、E在同一条直线上.求证: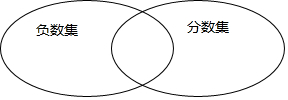 如图,两个圈分别表示负数集和分数集,请将3,0,$\frac{1}{2}$,-3$\frac{1}{3}$,-5,-3.4中符合条件的数填入圈中.
如图,两个圈分别表示负数集和分数集,请将3,0,$\frac{1}{2}$,-3$\frac{1}{3}$,-5,-3.4中符合条件的数填入圈中.