��Ŀ����
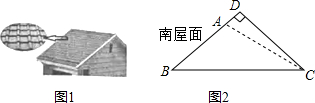
7�����Ķ����в��ϣ����⣺��ͼ1����ABC�У���ACB=90�㣬AC=BC��MN�ǹ���A��ֱ�ߣ�DB��MN�ڵ�D������CD��
��֤��BD+AD=$\sqrt{2}$CD
С����˼���������£�Ҫ֤BD+AD=$\sqrt{2}$CD����Ҫ��BD��ADת����ͬһ��ֱ���ϣ�������MN�Ͻ�ȡ
AE=BD��������EC����֤��ACE�͡�BCDȫ�ȣ��õ�CE=CD���ҡ�ACE=��BCD���ɴ��Ƴ���CDEΪ����ֱ�������Σ���֪DE=$\sqrt{2}$CD�����ǽ��۵�֤��
С�ϵ�˼���������£�Ҫ֤BD+AD=$\sqrt{2}$CD����Ҫ������CDΪ���ĵ���ֱ�������Σ����Թ���C��CE��CD��MN�ڵ�E����֤��ACE�͡�BCDȫ�ȣ��õ�CE=CD����AE=BD���ɴ��Ƴ���CDEΪ����ֱ�������Σ���֪BD+AD=$\sqrt{2}$CD�����ǽ��۵�֤��

����ο�С����С�ϵ�˼�����̽����������⣺
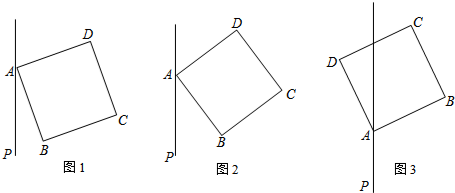
��1����ͼ1�е�ֱ��MN�Ƶ�A��ת��ͼ2��ͼ3������λ��ʱ�������������䣬����BD��AD��CD֮���������ϵ����ѡ������һ��ͼ�μ���֤����
��2����ֱ��MN�Ƶ�A��ת�Ĺ����У���ͼ3�У�����BCD=30�㣬BD=$\sqrt{2}$ʱ����CD�ij��ȣ�
���� ��1������C��CE��CB�ڵ�C����MN���ڵ�E��֤����ACE�ա�DCB�����ECBΪ����ֱ�������Σ��ݴ˼��ɵõ�BE=$\sqrt{2}$CB������BE=AB-AE����֤�ã�
��2������B��BH��CD�ڵ�H��֤����BDH�ǵ���ֱ�������Σ����DH�ij�����ֱ�ǡ�BCH�У�����ֱ����������30���������Ե�ֱ�DZߵ���б�ߵ�һ�룬������ã�
��� �⣺��1����ͼ2��BD-AD=$\sqrt{2}$CD��
��ͼ3��AD-BD=$\sqrt{2}$CD��
֤��ͼ2��С����˼����������
��ֱ��MN�Ͻ�ȡAE=BD������CE��
��AC��BD�ཻ�ڵ�F��
��BD��MN��
���ADB=90�㣬
���CAE+��AFD=90�㣮
�ߡ�ACB=90�㣬
���1+��BFC=90�㣮
�ߡ�AFD=��BFC��
���CAE=��1��
�ڡ�ACE�͡�BCD��
$\left\{\begin{array}{l}{AE=BD}\\{��CAE=��CBD}\\{AC=BC}\end{array}\right.$��
���ACE�ա�BCD��SAS����
��CE=CD����ACE=��BCD��
���ACE-��ACD=��BCD-��ACD��
����2=��ACB=90��
��Rt��CDE��
��CD2+CE2=DE2��
��2CD2=DE2��
��DE=$\sqrt{2}$CD��
��DE=AE-AD=BD-AD��
��BD-AD=$\sqrt{2}$CD��
С�ϵ�˼���������£���ͼ3 ��
��
����C��CE��CD��MN�ڵ�E��
���DCE=90�㣮
�ߡ�ACB=90�㣬
���DCE+��ACD=��ACB+��ACD��
����ACE=��BCD��
��AC��BD�ཻ�ڵ�F��
��DB��MN��
���ADB=90�㣮
���CAE+��AFD=90�㣬��DBC+��BFC=90�㣮
�ߡ�AFD=��BFC��
���CAE=��DBC��
�ڡ�ACE�͡�BCD��
$\left\{\begin{array}{l}{��CAE=��DBC}\\{AC=BC}\\{��ACE=��BCD}\end{array}\right.$��
���ACE�ա�BCD��ASA����
��CE=CD��AE=BD��
��Rt��CDE��
��CD2+CE2=DE2��
��2CD2=DE2��
��DE=$\sqrt{2}$CD��
��DE=AE-AD=BD-AD��
��BD-AD=$\sqrt{2}$CD��
֤������ͼ3��С����˼����������
��ֱ��MN�Ͻ�ȡAE=BD������CE��
��AD��BC�ཻ�ڵ�F��
�ߡ�ACB=90�㣬
���CAN+��AFC=90�㣮
��BD��MN��
���ADB=90�㣬��CBD+��BFD=90�㣮
�ߡ�AFC=��BFD��
���CAN=��CBD��
�ڡ�ACE�͡�BCD�У�
$\left\{\begin{array}{l}{AE=BD}\\{��CAN=��CBD}\\{AC=BC}\end{array}\right.$��
���ACE�ա�BCD��SAS����
��CE=CD����ACE=��BCD��
���ACE+��BCE=��BCD+��BCE��
����ECD=��ACB=90�㣮
��Rt��CDE��
��CD2+CE2=DE2��
��2CD2=DE2��
��DE=$\sqrt{2}$CD��
��DE=AD-AE=AD-BD��
��AD-BD=$\sqrt{2}$CD��
С�ϵ�˼���������£���ͼ3��
����C��CE��CD��MN�ڵ�E��
���DCE=90�㣮
�ߡ�ACB=90�㣬
���ACB-��ECB=��DCE-��ECB��
����ACE=��BCD
��AD��BC�ཻ�ڵ�F��
��DB��MN��
���ADB=90�㣮
���CAN+��AFC=90�㣬��CBD+��BFD=90�㣮
�ߡ�AFC=��BFD��
���CAE=��CBD��
�ߡ�ACE+��ECF=90�㣬��ECF+��BCD=90�㣬
���ACE=��BCD��
�ڡ�ACE�͡�BCD��
$\left\{\begin{array}{l}{��CAN=��CBD}\\{AC=BC}\\{��ACE=��BCD}\end{array}\right.$
���ACE�ա�BCD��ASA����
��CE=CD��AE=BD��
��Rt��CDE��CD2+CE2=DE2��
��2CD2=DE2��
��DE=$\sqrt{2}$CD��
��DE=AD-AE=AD-BD��
��AD-BD=$\sqrt{2}$CD��
��2��MN���Ƶ�A��ת�����У���û��ָ�������������
���ۺ��˵�һ��ͼ�͵ڶ���ͼ�������
���ǵ�1��ͼ��
�ߡ�ACE�ա�DCB��CE=CD��
���ECDΪ����ֱ�������Σ�
���AEC=45��=��CBD��
��D��DH��CB�����DHBΪ����ֱ��������
BD=$\sqrt{2}$BH��
��BH=DH=1��
ֱ�ǡ�CDH�У���DCH=30�㣬
BH=1����CH=$\sqrt{3}$��
��CD=$\sqrt{3}$+1
���ǵڶ���ͼ��
��B��BH��CD��CD�ӳ�����H��
�ⷨ�������棬CH=$\sqrt{3}$��DH=1��CD=$\sqrt{3}$-1��
�ʴ�Ϊ��$\sqrt{3}$��1
���� �����Ǽ��α任�ۺ��⣬��Ҫ������ȫ�������ε����ʺ��ж���Ӧ�ã�ע�⣺ȫ�������ε��ж�������SAS��ASA��AAS��SSS��ȫ�������ε�������ȫ�������εĶ�Ӧ����ȣ���Ӧ����ȣ��Ȿ��Ĺؼ������������ߣ�����ȫ�������Σ�

 ������������ϵ�д�
������������ϵ�д�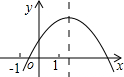 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ�
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ���4ac��b2����a+c��b����2a+b��0��
������ȷ���У�������
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �٢ڢ� |
| A�� | 5 | B�� | 4 | C�� | 2 | D�� | 6 |
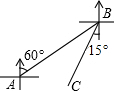 ��ͼ��ij�˴�A�������ƫ��60�㷽���ߵ�B�㣬�ٴ�B���������ƫ��15�㷽���ߵ�C�㣬���ABC���ڣ�������
��ͼ��ij�˴�A�������ƫ��60�㷽���ߵ�B�㣬�ٴ�B���������ƫ��15�㷽���ߵ�C�㣬���ABC���ڣ�������| A�� | 75�� | B�� | 105�� | C�� | 45�� | D�� | 135�� |