Question

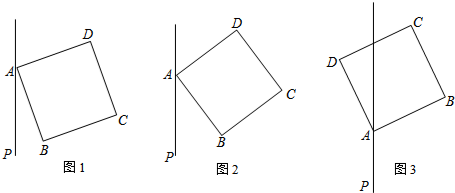
16．如图，将正方形ABCD从AP的位置（AB与AP重合）绕着点A逆时针方向旋转∠α的度数，作点B关于直线AP的对称点E，连接BE、DE，直线DE交直线AP于点F．
（1）如图1，若∠α=15°，求∠ADF的度数；
（2）如图2，若45°＜∠α＜90°，探索线段AB、FE、FD之间的数量关系，并证明；
（3）如图3，若90°＜∠α＜135°，（2）中的结论还成立吗？并说明理由．

Answer 1

分析 （1）先求得∠EAD的度数，然后再由旋转的性质和轴对称的性质证明AE=AD，最后依据等腰三角形的性质和三角形的内角和定理求解即可；
（2）连接BF、BD．由（1）∠ADF=∠AEF，结合旋转的性质可得到∠ADF=∠ABF，接下来，由四边形的内角和是360°可证明∠FBD=90°，最后在三角形BDF和△ABD中依据勾股定理可得到EF、DF、AB的关系；
（3）连接BD．由轴对称的性质和旋转的性质可证明；∠FEA=∠FBA，AE=AD．接下来，在四边形FDAB中，依据四边形的内角和定理证明∠DFB=90°，最后在三角形BDF和△ABD中依据勾股定理可得到EF、DF、AB的关系．

解答 解：（1）如图1所示：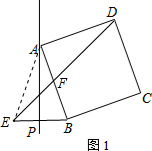

由题意得，∠BAP=∠EAP=15°，
∴∠EAD=∠EAB+∠BAD=120°．
∵AE=AB=AD，
∴AE=AD．
∴∠AED=∠ADE．
∴∠ADF=$\frac{1}{2}$（180°-120°）=30°．
（2）FE²+FD²=2AB²，
理由：如图2所示；连接BF、BD．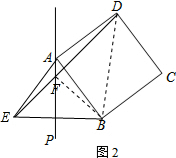

∵点E与点B关于AP对称，
∴∠AEF=∠ABF，EF=FB．
又∵∠ADE=∠AED，
∴∠ADF=∠ABF．
∵∠FDC=∠ADC-∠ADF，∠FBC=∠FBA+∠ABC，
∴∠FDC+∠FBC=180°．
∴∠DFB+DCB=180°．
∴∠DAB=∠DFB=90°．
∴BD²=FB²+DF²．
又∵EF=BF，
∴BD²=EF²+DF²．
∵∠DAB=90°，AD=AB，
∴BD²=2AB²．
∴EF²+DF²=2AB²．
（3）成立．
理由；如图3所示：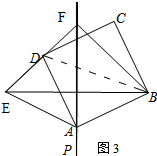

由轴对称的性质可知；∠FEA=∠FBA，AE=AB，
又∵AE=AB=AD，
∴AE=AD．
∴∠AED=∠ADE．
∴∠ADE=∠ABF．
∵∠ADE+∠FDA=180°，
∴∠ABF+∠FDA=180°．
∴∠DFB+∠DAB=180°．
∵∠DAB=90°，
∴∠DFB=90°．
∴DF²+BF²=BD²．
∵EF=BF．
∴DF²+EF²=BD²．
∵在Rt△ABD中，AB=AD，
∴DB²=2AB²．
∴DF²+EF²=2AB²．

点评 本题考查的是正方形的性质以及勾股定理和等腰三角形的性质、轴对称图形的性质、旋转的性质，四边形的内角和是360°，证得三角形BDF为直角三角形、三角形AED为等腰三角形是解题的关键．