题目内容
【题目】已知,![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]()
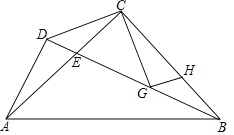
![]() 如图①,求证:
如图①,求证:![]() ;
;
![]() 如图②,将
如图②,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .连接
.连接![]() .
.
①若![]() ,求
,求![]() 的长;
的长;
②若![]() ,在图②的旋转过程中,当
,在图②的旋转过程中,当![]() 时,直接写出旋转角
时,直接写出旋转角![]() 的大小.
的大小.

【答案】![]() 证明见解析;(2)①6,②当旋转角
证明见解析;(2)①6,②当旋转角![]() 为
为![]() 或
或![]() .
.
【解析】
(1)根据等腰三角形两底角相等![]() ,再根据平行线的性质得出,
,再根据平行线的性质得出,![]() ,
,![]() ,得出
,得出![]() ,进一步得出结论;
,进一步得出结论;
(2)求出![]() ,再根据旋转的性质可得
,再根据旋转的性质可得![]() ,
,![]() ,然后利用“边角边”证明
,然后利用“边角边”证明![]() 和
和![]() 全等,根据全等三角形对应边相等证明即可;
全等,根据全等三角形对应边相等证明即可;
(3)把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 与过点
与过点![]() 与
与![]() 平行的直线相交于
平行的直线相交于![]() 、
、![]() ,然后分两种情况,根据等腰梯形的性质和等腰三角形的性质分别求解即可.
,然后分两种情况,根据等腰梯形的性质和等腰三角形的性质分别求解即可.
![]() 证明:∵
证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() 解:①由旋转的性质得,
解:①由旋转的性质得,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ;
;
②由![]() 可知
可知![]() ,
,
所以,在![]() 绕点
绕点![]() 逆时针旋转过程中,点
逆时针旋转过程中,点![]() 经过的路径(圆弧)与过点
经过的路径(圆弧)与过点![]() 且与
且与![]() 平行的直线
平行的直线![]() 相交于点
相交于点![]() 、
、![]() ,如图,
,如图,
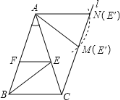
①当点![]() 的像
的像![]() 与点
与点![]() 重合时,四边形
重合时,四边形![]() 是等腰梯形,
是等腰梯形,
所以,![]() ,
,
又∵![]() ,
,
∴![]() ;
;
②当点![]() 的像
的像![]() 与点
与点![]() 重合时,
重合时,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,当旋转角![]() 为
为![]() 或
或![]()

练习册系列答案
相关题目