题目内容
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的横坐标为4.
的横坐标为4.
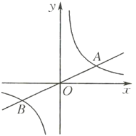
(1)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(2)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),若由点
在第一象限),若由点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点组成的四边形面积为24,求点
为顶点组成的四边形面积为24,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)将x=4代入一次函数解析式求出y的值,确定出A的坐标,将A坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;将C纵坐标代入反比例解析式求出横坐标,确定出C坐标,即CD与OD的长,三角形AAOC面积=三角形COD面积+梯形AEDC面积-三角形AOE面积,求出即可;
(2)设![]() ,即OM=m,PM=
,即OM=m,PM=![]() ,分两种情况考虑:若P在A的左侧,如图所示,作PM⊥x轴,AN⊥x轴,由四边形APBQ面积为24,且为平行四边形,得到三角形AOP面积为6,根据三角形POM面积+梯形ANMP面积-三角形AON面积,列出关于x的方程,求出方程的解得到x的值,确定出此时P的坐标;若P在A的右侧,同理可得P的坐标.
,分两种情况考虑:若P在A的左侧,如图所示,作PM⊥x轴,AN⊥x轴,由四边形APBQ面积为24,且为平行四边形,得到三角形AOP面积为6,根据三角形POM面积+梯形ANMP面积-三角形AON面积,列出关于x的方程,求出方程的解得到x的值,确定出此时P的坐标;若P在A的右侧,同理可得P的坐标.
(1)∵点![]() 的横坐标为4
的横坐标为4
∴把![]() 代入
代入![]() 中,得
中,得![]()
∴![]()
∵点![]() 是直线
是直线![]() 与双曲线
与双曲线![]() 的交点
的交点
∴![]()
∴双曲线的解析式为![]()
如图所示,过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() 、
、![]()
∵点![]() 在双曲线
在双曲线![]() 上
上
∴当![]() 时,
时,![]()
∴点![]() 的坐标为
的坐标为![]()
∵点![]() 、
、![]() 在双曲线
在双曲线![]() 上
上
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
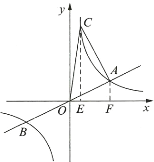
(2)∵反比例函数图像是关于原点![]() 的中心对称图形
的中心对称图形
∴![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]()
设点![]() 的横坐标为
的横坐标为![]() (
(![]() 且
且![]() )
)
∴![]()
过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() 、
、![]()
∵点![]() 、
、![]() 在双曲线上
在双曲线上
∴![]()
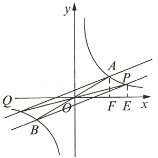
若![]() ,如图所示:
,如图所示:
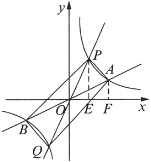
∵![]()
∴![]()
即![]()
∴![]() ,
,![]() (舍去)
(舍去)
∴![]()
若![]() ,如图所示:
,如图所示:
∵![]()
∴![]()
即![]()
∴![]() ,
,![]() (舍去)
(舍去)
∴![]()
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目