题目内容
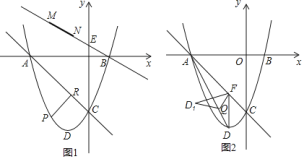
【题目】如图![]() ,已知抛物线
,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 为顶点.
为顶点.
![]() 求直线
求直线![]() 的解析式和顶点
的解析式和顶点![]() 的坐标;
的坐标;
![]() 已知
已知![]() ,点
,点![]() 是直线
是直线![]() 下方的抛物线上一动点,作
下方的抛物线上一动点,作![]() 于点
于点![]() ,当
,当![]() 最大时,有一条长为
最大时,有一条长为![]() 的线段
的线段![]() (点
(点![]() 在点
在点![]() 的左侧)在直线
的左侧)在直线![]() 上移动,首尾顺次连接
上移动,首尾顺次连接![]() 、
、![]() 、
、![]() 、
、![]() 构成四边形
构成四边形![]() ,请求出四边形
,请求出四边形![]() 的周长最小时点
的周长最小时点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,过点
,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 点是线段
点是线段![]() 上一动点,将
上一动点,将![]() 沿直线
沿直线![]() 折叠至
折叠至![]() ,是否存在点
,是否存在点![]() 使得
使得![]() 与
与![]() 重叠部分的图形是直角三角形?若存在,请求出
重叠部分的图形是直角三角形?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】![]() 直线
直线![]() 的解析式为
的解析式为![]() ,点
,点![]() 坐标
坐标![]() .
.![]()
![]() .
.![]() 存在.当
存在.当![]() 与
与![]() 重叠部分的图形是直角三角形时,
重叠部分的图形是直角三角形时,![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)分别令x=0和y=0可求解出ABC三点的坐标,利用待定系数法求解直线AC的解析式;将二次函数一般式化为顶点式即可求解D点坐标;
(2)由于AC长度固定,故当PR最大时,△APC的面积最大,由图像可知![]() ,设P(m,m2+2m-3),代入其中可求解m从而确定P点坐标;将点
,设P(m,m2+2m-3),代入其中可求解m从而确定P点坐标;将点![]() 沿
沿![]() 方向平移
方向平移![]() 个单位得到
个单位得到![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,此时四边形
,此时四边形![]() 的最长最小;
的最长最小;
(3)分三种情况进行讨论:当![]() 时,重叠部分是RT△FKQ;当
时,重叠部分是RT△FKQ;当![]() 时,重叠部分是RT△FQD;、当
时,重叠部分是RT△FQD;、当![]() 时,重叠部分是RT△QMF.
时,重叠部分是RT△QMF.
![]() 对于抛物线
对于抛物线![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,
∴![]() ,
,
∵抛物线![]() ,
,
∴顶点![]() 坐标为
坐标为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,则有
,则有![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,点
,点![]() 坐标
坐标![]() .
.
![]() 如图
如图![]() 中,设
中,设![]()

由题意,当![]() 最大时,
最大时,![]() 的面积最大,即四边形
的面积最大,即四边形![]() 的面积最大,
的面积最大,
∵
![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 的面积最大,即
的面积最大,即![]() 最长,
最长,
∴![]() ,
,
将点![]() 沿
沿![]() 方向平移
方向平移![]() 个单位得到
个单位得到![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,此时四边形
,此时四边形![]() 的最长最小,
的最长最小,
∵直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,
,
由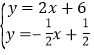 解得
解得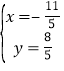 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
由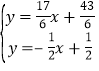 解得
解得 ,
,
∴![]() ,将点
,将点![]() 向下平移
向下平移![]() 个单位,向右平移
个单位,向右平移![]() 个单位得到
个单位得到![]() ,
,
∴![]() .
.
![]() 存在.
存在.
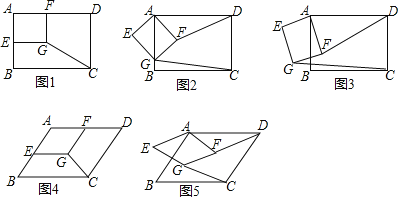
①如图![]() 中,当
中,当![]() 时,重叠部分是
时,重叠部分是![]() ,作
,作![]() 于
于![]() .
.
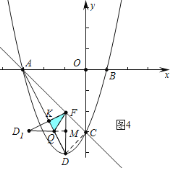
由题意可求得![]() ,容易求得
,容易求得![]() ,
,![]() ,
,![]() ,
,![]() ,CD=
,CD=![]()
∵AD2=20=AC2+CD2,
∴∠ACD=90°,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,设
,设![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]()
②如图![]() 中,当
中,当![]() 时,重叠部分是
时,重叠部分是![]() ,此时
,此时![]() .
.
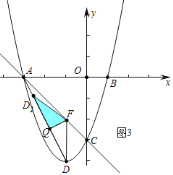
③如图![]() 中,当
中,当![]() 时,重叠部分是
时,重叠部分是![]() .
.
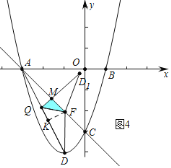
设![]() ,在
,在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,当![]() 与
与![]() 重叠部分的图形是直角三角形时,
重叠部分的图形是直角三角形时,![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案