Question

【题目】在平面直角坐标系中，△ABC三个顶点的坐标为：A（﹣3，2），B（﹣4，﹣3）C（﹣1，﹣1）

（1）若△A1B1C1与△ABC关于y轴对称，请写出点A1，B1，C1的坐标（直接写答案）：A1　　；B1，　　；C1　　；

（2）△ABC的面积为　　；

（3）在y轴上画出点P，使PB+PC最小．

Answer 1

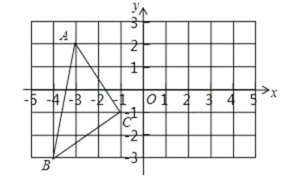
【答案】（1）（3，2）、（4，﹣3）、（1，﹣1）；（2）6.5；（3）见解析．

【解析】

（1）根据点关于y轴对称的性质“横坐标变为相反数，纵坐标不变”即可得；

（2）如图可知（见解析），利用长方形和三角形面积公式即可得；

（3）由题意可得y轴是线段的垂直平分线，则，因此；又根据三角形的三边关系得，所以当三点共线时，最小，且最小值为.

（1）根据点关于y轴对称的性质得：；

（2）如图可知，

则；

（3）由题意可得y轴是线段的垂直平分线，则

因此

由三角形的三边关系得

故当三点共线时，最小，且最小值为

连接，与y轴的交点即为所求点P（如图所示）.