题目内容
 如图,在Rt△ABC中,∠C=90°,AC=BC=a,延长CA到D,使AD=AB,连接BD.
如图,在Rt△ABC中,∠C=90°,AC=BC=a,延长CA到D,使AD=AB,连接BD.(1)求∠D的度数;
(2)求tanD的值;
(3)利用上面的结果计算:tan22.5°•cos45°+
| (sin45°-tan22.5°)2 |
考点:解直角三角形
专题:计算题
分析:(1)先判断△ACB为等腰直角三角形,则∠BAC=45°,根据等腰三角形的性质由AB=AD得∠D=∠ABD,在利用三角形外角性质可计算出∠D=
∠BAC=22.5°;
(2)由于△ACB为等腰直角三角形,则AB=
AC=
a,所以AD=
a,则CD=DA+AC=(
+1)a,然后在Rt△BDC中利用正切的定义求解;
(3)先根据二次根式的性质化简得到原式=tan22.5°•cos45°+|sin45°-tan22.5°|,再把(2)中的计算结果和45°的正余弦值代入进行计算即可.
| 1 |
| 2 |
(2)由于△ACB为等腰直角三角形,则AB=
| 2 |
| 2 |
| 2 |
| 2 |
(3)先根据二次根式的性质化简得到原式=tan22.5°•cos45°+|sin45°-tan22.5°|,再把(2)中的计算结果和45°的正余弦值代入进行计算即可.
解答:解:(1)∵∠C=90°,AC=BC=a,
∴△ACB为等腰直角三角形,
∴∠BAC=45°,
∵AB=AD,
∴∠D=∠ABD,
而∠BAC=∠D+∠ABD,
∴∠D=
∠BAC=22.5°;
(2)∵△ACB为等腰直角三角形,
∴AB=
AC=
a,
∴AD=
a,
∴CD=DA+AC=(
+1)a,
在Rt△BDC中,tanD=
=
=
-1;
(3)原式=tan22.5°•cos45°+|sin45°-tan22.5°|
=(
-1)•
+|
-(
-1)|
=1-
+1-
=2-
.
∴△ACB为等腰直角三角形,
∴∠BAC=45°,
∵AB=AD,
∴∠D=∠ABD,
而∠BAC=∠D+∠ABD,
∴∠D=
| 1 |
| 2 |
(2)∵△ACB为等腰直角三角形,
∴AB=
| 2 |
| 2 |
∴AD=
| 2 |
∴CD=DA+AC=(
| 2 |
在Rt△BDC中,tanD=
| BC |
| DC |
| a | ||
(
|
| 2 |
(3)原式=tan22.5°•cos45°+|sin45°-tan22.5°|
=(
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
=1-
| ||
| 2 |
| ||
| 2 |
=2-
| 2 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
某商店在进一批水果时,已按原价x打了75折,它想在价目牌上写上标价y,然后进行8折促销,而且要保证获利25%
(1)求y与x之间的函数关系式;
(2)一位顾客看到价目牌上为15元/斤,则其实际进价是多少?
(1)求y与x之间的函数关系式;
(2)一位顾客看到价目牌上为15元/斤,则其实际进价是多少?
在实数
,
,0.1414,
,-
,0.1010010001…,-
,0,1-
,
,|
-1|中,有几个无理数( )
| π |
| 2 |
| 22 |
| 7 |
| 3 | 9 |
| 5 |
| 2 |
|
| 2 |
| ||
| 2 |
| 4 |
| A、3个 | B、4个 | C、5个 | D、6个 |
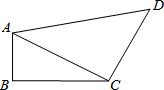 如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且∠ABC=90°,连接AC.
如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且∠ABC=90°,连接AC. 如图,在△ABC中,CF:EF:BE=3:2:1,BD:AD=2:3.求CH:HG:DG的比.
如图,在△ABC中,CF:EF:BE=3:2:1,BD:AD=2:3.求CH:HG:DG的比. 如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.