题目内容
14.阅读下面材料:小乔遇到了这样一个问题:如图1,在Rt△ABC中,∠C=90°,D,E分别为CB,CA边上的点,且AE=BC,BD=CE,BE与AD的交点为P,求∠APE的度数;
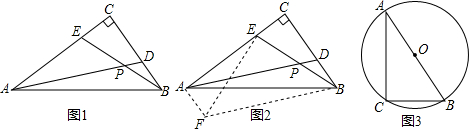
小乔发现题目中的条件分散,想通过平移变换将分散条件集中,如图2,过点B作BF∥AD且BF=AD,连接EF,AF,从而构造出△AEF与△CBE全等,经过推理和计算能够使问题得到解决(如图2).
请回答:∠APE的度数为45°.
参考小乔同学思考问题的方法,解决问题:
如图3,AB为⊙O的直径,点C在⊙O上,D、E分别为CB,CA上的点,且AE=$\frac{1}{2}$BC,BD=$\frac{1}{2}CE$,BE与AD交于点P,在图3中画出符合题意的图形,并求出sin∠APE的值.
分析 (1)利用平行四边形的判定与性质得出AF=BD,进而得出△AEF≌△CBE(SAS),即可得出:∠APE的度数;
(2)根据题意首先得出△AEF∽△CBE,进而得出tan∠FBE=$\frac{EF}{BE}$=$\frac{1}{2}$,即可求出sin∠APE的值.
解答 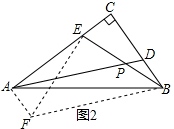 解:(1)如图2,过点B作BF∥AD且BF=AD,连接EF,AF,
解:(1)如图2,过点B作BF∥AD且BF=AD,连接EF,AF,
∵BF∥AD且BF=AD,
∴四边形AFBD是平行四边形,
∴AF=BD,
在△AEF和△CBE中
∵$\left\{\begin{array}{l}{AE=BC}\\{∠FAE=∠C}\\{AF=EC}\end{array}\right.$,
∴△AEF≌△CBE(SAS),
∴EF=BE,∠AEF+∠CEB=90°,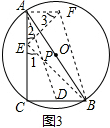
∴∠EBF=45°,
∵AD∥BF,
∴∠APE=45°;
故答案为:45°;
(2)如图3,过点B作FB∥AD且FB=AD,连接EF和AF,
∴四边形AFBD是平行四边形,
∠APE=∠FBE,AF=DB,
∵AB是⊙O直径,∴∠C=90°,
∴∠FAE=∠BCE=90°,
∵CE=2BD,BC=2AE,
∴CE=2AF,∴$\frac{CE}{AF}$=$\frac{BC}{EA}$=2,
∴△AEF∽△CBE,
∴$\frac{EF}{BE}$=$\frac{1}{2}$,∠1=∠3,
又∵∠2+∠3=90°,
∴∠1+∠2=90°,即∠FEB=90°,
在Rt△BEF中,∠FEB=90°,
∴tan∠FBE=$\frac{EF}{BE}$=$\frac{1}{2}$,
又∵∠APE=∠FBE,
∴sin∠APE=$\frac{\sqrt{5}}{5}$.
点评 此题主要考查了平行四边形的性质与判定以及全等三角形的判定与性质和相似三角形的判定与性质等知识,做出正确辅助线构造平行四边形是解题关键.

 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2014次“移位”后,则他所处顶点的编号是3.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2014次“移位”后,则他所处顶点的编号是3. 如图所示,一次函数y=kx+b的图象经过A、B两点,则kx+b>0的解集是x>-3.
如图所示,一次函数y=kx+b的图象经过A、B两点,则kx+b>0的解集是x>-3.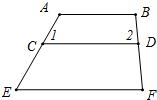 如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.
如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.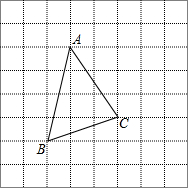 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个最小的圆去覆盖△ABC,请你在如图所示的网格中,用直尺画出该圆的圆心(保留作图痕迹),并简要说明画图的方法(不要求证明)填什么.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个最小的圆去覆盖△ABC,请你在如图所示的网格中,用直尺画出该圆的圆心(保留作图痕迹),并简要说明画图的方法(不要求证明)填什么.