题目内容
3.如图1,已知抛物线y=-x2+bx+c经过点A(1,0)和点B(-3,0),该抛物线与y轴的交点为C,顶点是D.(1)求此抛物线的解析式和顶点D的坐标;
(2)求△ACD的面积;
(3)如图2,点E直线y=-x上一动点,在所求抛物线上是否存在点F,使以E、F、C、O为顶点的四边形是平行四边形?若存在,请求出点E的坐标;若不存在,请说明理由.
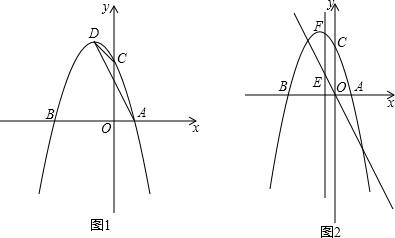
分析 (1)把A(1,0)和点B(-3,0)代入抛物线的解析式得$\left\{\begin{array}{l}{-1+b+c=0}\\{-9-3b+c=0}\end{array}\right.$,解方程组即可.
(2)如图1中,连接OD、AC.根据S△ACD=S△COD+S△AOC-S△AOD计算即可.
(3)分两种情形①当EF=OC,EF∥CO时,E、F、C、O为顶点的四边形是平行四边形,设E(m,-m),则F(m,-m2-2m+3);②当OC为对角线时,设OC的中点为G,则G(0,$\frac{3}{2}$),设E(m,-m),则F(-m,3+m,),分别列出方程求解即可.
解答 解:(1)把A(1,0)和点B(-3,0)代入抛物线的解析式得$\left\{\begin{array}{l}{-1+b+c=0}\\{-9-3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点D坐标(-1,4).
(2)如图1中,连接OD、AC.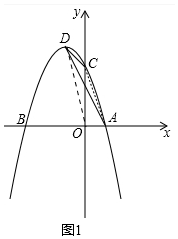
∵C(0,3),
∴S△ACD=S△COD+S△AOC-S△AOD
=$\frac{1}{2}$×3×1+$\frac{1}{2}$×3×1-$\frac{1}{2}$×1×4
=1.
(3)如图2中,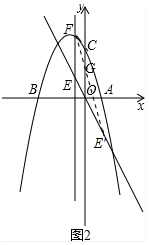
①当EF=OC,EF∥CO时,E、F、C、O为顶点的四边形是平行四边形,设E(m,-m),则F(m,-m2-2m+3),
则有-m2-2m+3-(-m)=3或-m-(-m2-2m+3)=3,
解得m=-1或0(舍弃)或m=-3 或2,
∴E(-1,1)或(-3,3)或(2,-2).
②当OC为对角线时,设OC的中点为G,则G(0,$\frac{3}{2}$),设E(m,-m),则F(-m,3+m,),
∴3+m=-m2+2m+3,
∴m=1,
∴E(1,-1),
综上所述,当点E坐标为E(-1,1)或(-3,3)或(2,-2)或(1,-1)时,抛物线上存在点F,使以E、F、C、O为顶点的四边形是平行四边形.
点评 本题考查二次函数综合题、三角形的面积、平行四边形的判定和性质等知识,解题的关键是学会用分割法求三角形面积,学会分类讨论,学会用方程的思想思考问题,属于中考压轴题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案 如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )
如图,已知∠ACB=60°,PC=12,点M,N在边CB上,PM=PN.若MN=3,则CM的长为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
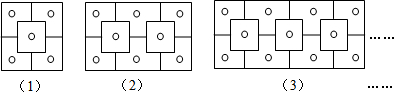
| A. | 23个 | B. | 24个 | C. | 25个 | D. | 26个 |
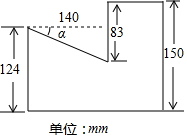 一个零件的轴截面如图所示,根据图中尺寸求倾角α(精确到1′).
一个零件的轴截面如图所示,根据图中尺寸求倾角α(精确到1′). 已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.
已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点. 如图,在?ABCD中,对角线AC与BD相交于点O,BD⊥AD,AB=10,AD=8.求OB的长度及?ABCD的面积.
如图,在?ABCD中,对角线AC与BD相交于点O,BD⊥AD,AB=10,AD=8.求OB的长度及?ABCD的面积.