题目内容
 在△ABC中,AD为∠BAC的平分线,∠ABC=2∠C,猜想AB、BD和AC之间的关系,并说明理由.
在△ABC中,AD为∠BAC的平分线,∠ABC=2∠C,猜想AB、BD和AC之间的关系,并说明理由.考点:全等三角形的判定与性质
专题:
分析:在AC上截取AE=AB,然后利用“边角边”证明△ABD和△AED全等,根据全等三角形对应边相等可得BD=DE,全等三角形对应角相等可得∠AED=∠ABC,再求出∠C=∠CDE,根据等角对等边可得CE=DE,从而得到BD=CE,然后根据AC=AE+CE等量代换即可得证.
解答: 解:如图,在AC上截取AE=AB,
解:如图,在AC上截取AE=AB,
∵AD为∠BAC的平分线,
∴∠BAD=∠CAD,
在△ABD和△AED中,
,
∴△ABD≌△AED(SAS),
∴BD=DE,∠AED=∠ABC,
∵∠ABC=2∠C,
∴∠AED=2∠C,
∴∠C=∠CDE,
∴CE=DE,
∴BD=CE,
∵AC=AE+CE,
∴AB+BD=AC.
 解:如图,在AC上截取AE=AB,
解:如图,在AC上截取AE=AB,∵AD为∠BAC的平分线,
∴∠BAD=∠CAD,
在△ABD和△AED中,
|
∴△ABD≌△AED(SAS),
∴BD=DE,∠AED=∠ABC,
∵∠ABC=2∠C,
∴∠AED=2∠C,
∴∠C=∠CDE,
∴CE=DE,
∴BD=CE,
∵AC=AE+CE,
∴AB+BD=AC.
点评:本题考查了全等三角形的判定与性质,利用“截长法”作辅助线构造成全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
正方形内有一点P到各边的距离为2,3,4,5,则正方形的面积为( )
| A、36 | B、49 | C、64 | D、81 |
 如图所示,某水库大坝的横断面是梯形,坝顶AD宽2.5m,坝高4m,背水坡的坡度是1:1,迎水坡的坡度是1:1.5,求坝底宽BC.
如图所示,某水库大坝的横断面是梯形,坝顶AD宽2.5m,坝高4m,背水坡的坡度是1:1,迎水坡的坡度是1:1.5,求坝底宽BC.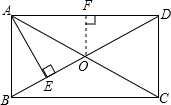 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长.