题目内容
8.已知an=(-1)n+1,当n=1时,a1=0;当n=2时,a2=2;当n=3时,a3=0,…;则a1+a2+a3+…+a2017的值为( )| A. | 1008 | B. | 1010 | C. | 2016 | D. | 2017 |
分析 根据指数幂的知识,当n为奇数时,(-1)n=-1;当n为偶数时,(-1)n=1,找出此规律,得出2017个数中有1008个2相加,1009个0相加,再进行计算即可得出答案.
解答 解:∵当n=1时,a1=0,
当n=2时,a2=2,
当n=3时,a3=0,
当n=4时,a2=2,
…,
∴a1+a2+a3+…+a2017=0+2+0+2+…+0=2×1008=2016;
故选C.
点评 本题考查学生分析数据,总结、归纳数据规律的能力,关键是找出规律,要求学生要有一定的解题技巧.本题的关键是找到规律:当n为奇数时,(-1)n=-1;当n为偶数时,(-1)n=1.

练习册系列答案
相关题目
3.在a3•a2•( )=a12中,括号内应填写的代数式是( )
| A. | a7 | B. | a6 | C. | a8 | D. | a3 |
17.已知两个整数a,b,满足0<b<a<10,且$\frac{9a}{a+b}$是整数,那么数对(a,b)有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
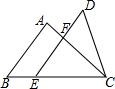 如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )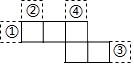 由五个全等正方形组成的图形如图所示,将一个同样大小的正方形放在图中的①、②、③、④某一位置,所组成的图形不是正方体表面展开图的是( )
由五个全等正方形组成的图形如图所示,将一个同样大小的正方形放在图中的①、②、③、④某一位置,所组成的图形不是正方体表面展开图的是( ) 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.