Question

4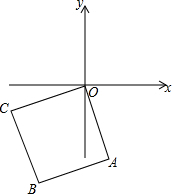．已知正方形OABC在直角坐标系中（如图），A（1，-3），求点B、C的坐标．

Answer 1

分析 作AD⊥x轴于D，CE⊥x轴于E，BF⊥CE于F，如图，根据正方形的性质得OC=OA，∠AOC=90°，则利用同角的余角相等得∠OAD=∠EOC，则可根据“AAS”判断△COE≌△OAD，所以OE=AD=3，CE=OD=1，同样方法可证得△BFC≌△CEO，则BF=CE=1，CF=OE=3，然后利用第三象限点的坐标特征写出B、C点坐标．

解答 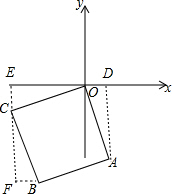解：作AD⊥x轴于D，CE⊥x轴于E，BF⊥CE于F，如图，
∵A点坐标为（1，-3），
∴OD=1，AD=3，
∵四边形ABCD为正方形，
∴OC=OA，∠AOC=90°，
∵∠EOC+∠AOD=90°，∠AOD+∠OAD=90°，
∴∠OAD=∠EOC，
在△COE和△OAD中
$\left\{\begin{array}{l}{∠CEO=∠DOA}\\{∠EOC=∠DAO}\\{CO=OA}\end{array}\right.$，
∴△COE≌△OAD，
∴OE=AD=3，CE=OD=1，
∴C（-3，-1），
同样方法可证得△BFC≌△CEO，
∴BF=CE=1，CF=OE=3，
∴B（-2，-4）．

点评 本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．解决本题的关键是利用正方形的性质构建全等三角形．