题目内容
10.正△ABC的边长为2,M是AB边上的中点,P是BC边上的任意一点,PA+PM的最大值是2+$\sqrt{3}$,最小值是$\sqrt{7}$.分析 作点M关于CB的对称点M′连接AM′、M′C,AM′交BC与点P,由等腰三角形三线合一的性质可知∠MCP=∠ACP=30°,由轴对称的性质可知∠MCP=∠M′CP,从而得到∠ACM′=90°,在Rt△AM′C中利用勾股定理可求得AM′的长,从而可求得PA+PM的最小值;如图2所示;当点P与点C重合时,PA+PM有最大值.
解答 解:如图1所示:作点M关于CB的对称点M′连接AM′、M′C.
∵点M与点M′关于BC对称,
∴MP=M′P,∠MCP=∠M′CP.
∵△ABC是正三角形,M是AB的中点,
∴MC=CM′,∠MCP=∠ACP=30°.
∴∠MCP=∠ACP=∠M′CP=30°.
∴CM′=MC=BC×cos30°=$2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴∠ACM′=90°.
∴AM′=$\sqrt{A{M}^{2}+M′{C}^{2}}$=$\sqrt{7}$.
∴PA+PM的最小值是$\sqrt{7}$.
如图2所示:当点P与点C重合时.PM+PA有最大值.
∵PM=$\sqrt{3}$,AP=2,
∴PA+PM=2+$\sqrt{3}$.
故答案为:2+$\sqrt{3}$;$\sqrt{7}$.
点评 本题主要考查的轴对称最短路径问题、勾股定理的应用、等腰三角形的性质,明确当点M′、P、A在一条直线上时,PM+PA有最小值,当点P与点C重合时,PM+PA有最大值是解题的关键.

练习册系列答案
相关题目
5.二次三项式-3x2+x+2>0的解集是( )
| A. | x>q或x<-$\frac{2}{3}$ | B. | 无解 | C. | -$\frac{2}{3}$<x<1 | D. | x>1 |
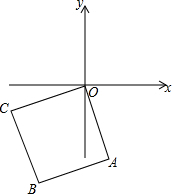 已知正方形OABC在直角坐标系中(如图),A(1,-3),求点B、C的坐标.
已知正方形OABC在直角坐标系中(如图),A(1,-3),求点B、C的坐标. 直线AB上一点,OM平分∠AOC,ON平分∠BOC,∠BON=28°,则∠BOC=56°,∠BOM=118°,图中互补的角有5对.
直线AB上一点,OM平分∠AOC,ON平分∠BOC,∠BON=28°,则∠BOC=56°,∠BOM=118°,图中互补的角有5对.