题目内容
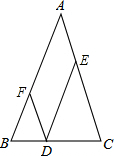 如图,点D、E、F分别在△ABC的边上,请从以下四个关系∠FDE=∠A,∠BFD=∠DEC,DE∥BA,DF∥CA中,选择三个适当的填写在横线上,使其形成一个真命题,并有步骤的证明这个命题.(证明过程中注明推理依据)
如图,点D、E、F分别在△ABC的边上,请从以下四个关系∠FDE=∠A,∠BFD=∠DEC,DE∥BA,DF∥CA中,选择三个适当的填写在横线上,使其形成一个真命题,并有步骤的证明这个命题.(证明过程中注明推理依据)如果
求证:
证明:
考点:平行线的判定与性质,命题与定理
专题:开放型
分析:利用∠FDE=∠A,DE∥BA得到DF∥CA:先根据平行线的性质由DE∥AB得到∠A=∠DEC,由于∠FDE=∠A,则∠FED=∠DEC,然后根据平行线的判定即可得到DF∥CA.
解答:已知:∠FDE=∠A,DE∥BA,
求证:DF∥CA.
证明:∵DE∥AB,
∴∠A=∠DEC,
∵∠FDE=∠A,
∴∠FED=∠DEC,
∴DF∥CA.
故答案为:∠FDE=∠A,DE∥BA;DF∥CA.
求证:DF∥CA.
证明:∵DE∥AB,
∴∠A=∠DEC,
∵∠FDE=∠A,
∴∠FED=∠DEC,
∴DF∥CA.
故答案为:∠FDE=∠A,DE∥BA;DF∥CA.
点评:本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等.

练习册系列答案
相关题目
已知2x-3y=1,用含x的代数式表示y正确的是( )
A、y=
| ||||
B、x=
| ||||
C、y=
| ||||
D、y=-
|
 如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度. 如图,在?ABCD中,E、F分别是AB,CD的中点,求证:DE=BF.
如图,在?ABCD中,E、F分别是AB,CD的中点,求证:DE=BF. 如图,某农场建一个矩形的养鸡场,鸡场的一边靠墙(墙长15m),另三边用40m长的木栏围成.
如图,某农场建一个矩形的养鸡场,鸡场的一边靠墙(墙长15m),另三边用40m长的木栏围成. 小刚家的住房结构如图(单位:米),小刚的爸爸打算把卧室、卫生间、厨房和客厅都铺上地砖,请你帮他算一算,至少需要买多少平方米的地砖?
小刚家的住房结构如图(单位:米),小刚的爸爸打算把卧室、卫生间、厨房和客厅都铺上地砖,请你帮他算一算,至少需要买多少平方米的地砖? 如图,一块含有45°角的直角三角板的一个顶点放在直尺的一边上,若∠1=30°,则∠2=
如图,一块含有45°角的直角三角板的一个顶点放在直尺的一边上,若∠1=30°,则∠2=