题目内容
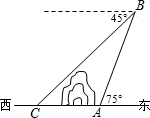 如图,在小山的东侧A处有一热气球,以每分钟10米的速度沿着仰角为75°的方向上升,20分钟后上升到B处,这时气球上的人发现在点A的正西方向俯角为45°的C处有一着火点,求气球的升空点A与着火点C之间的距离.(结果保留根号)
如图,在小山的东侧A处有一热气球,以每分钟10米的速度沿着仰角为75°的方向上升,20分钟后上升到B处,这时气球上的人发现在点A的正西方向俯角为45°的C处有一着火点,求气球的升空点A与着火点C之间的距离.(结果保留根号)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先过点A作AD⊥BC于点D,先求得∠ABD=30°,AB=10×20=200(m),在Rt△ABD中,利用三角函数的知识即可求得AD长,由平行线的性质求出∠BCA,易证得CD=AD,继而求得AC的长度.
解答:解:过点A作AD⊥BC于点D,
由题意得,BE∥AC,∠EBC=45°,∠BAD=75°,
∴∠ABD=30°,
∵AB=10×20=200(m),
在Rt△ABD中,
AD=ABsin∠ABD=
×200=100(m),
∵BE∥AC,
∴∠BCA=∠EBC=45°,
∴AC=
=
=100
(m),
即气球的升空点A与着火点C之间的距离为100
m.

由题意得,BE∥AC,∠EBC=45°,∠BAD=75°,
∴∠ABD=30°,
∵AB=10×20=200(m),
在Rt△ABD中,
AD=ABsin∠ABD=
| 1 |
| 2 |
∵BE∥AC,
∴∠BCA=∠EBC=45°,
∴AC=
| AD |
| sin45° |
| 100 | ||||
|
| 2 |
即气球的升空点A与着火点C之间的距离为100
| 2 |
点评:本题考查了仰角与俯角的定义.此题难度适中,注意能借助仰角与俯角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
 如图两个转盘,指针落在每一个数上的机会均等,则两个指针同时落在偶数上的概率是
如图两个转盘,指针落在每一个数上的机会均等,则两个指针同时落在偶数上的概率是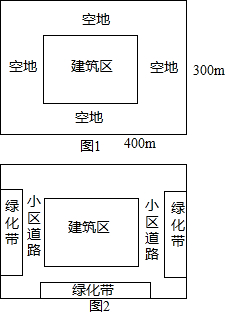 如图1,某小区的平面图是一个占地400×300平方米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形.如果要使四周的空地所占面积是小区面积的36%,南北空地等宽,东西空地等宽.
如图1,某小区的平面图是一个占地400×300平方米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形.如果要使四周的空地所占面积是小区面积的36%,南北空地等宽,东西空地等宽.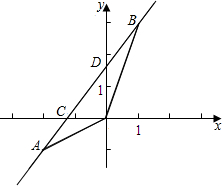 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.