题目内容
18.若a,b,c分别是直角三角形的三边长,给出下列结论:(a)长为a2,b2,c2的三条线段能组成直角三角形吗?为什么?
(2)长为2a,2b,2c的三条线段能组成直角三角形吗?为什么?
分析 由a,b,c分别是直角三角形的三边长(假设c是斜边),根据勾股定理得出a2+b2=c2,
(1)举反例不能得出(a2)2+(b2)2=(c2)2,由勾股定理的逆定理即可判断长为a2,b2,c2的三条线段不能组成直角三角形;
(2)由a2+b2=c2,根据等式的性质以及幂的乘方的性质可得(2a)2+(2b)2=(2c)2,由勾股定理的逆定理即可判断长为2a,2b,2c的三条线段能组成直角三角形.
解答 解:∵a,b,c分别是直角三角形的三边长(假设c是斜边),
∴a2+b2=c2,
(1)不能.理由如下:
令a=3,b=4,c=5,满足a2+b2=c2,
但是(a2)2+(b2)2=81+256=337,(c2)2=625,
∴(a2)2+(b2)2≠(c2)2,
∴长为a2,b2,c2的三条线段不能组成直角三角形;
(2)能.理由如下:
∵a2+b2=c2,
∴4a2+4b2=4c2,
即(2a)2+(2b)2=(2c)2,
∴长为2a,2b,2c的三条线段能组成直角三角形.
点评 本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.也考查了勾股定理.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
6.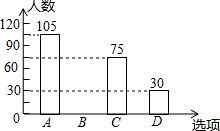 某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
请结合统计图表,回答下列问题:
(1)本次抽查的学生共300人,a=30%,并将条形统计图补充完整;
(2)如果该校学生有1800人,请你估计该校喜欢“唱歌”这项宣传方式的学生约有多少人?
 某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 绘画 | 25% |
| D | 演讲 | 10% |
(1)本次抽查的学生共300人,a=30%,并将条形统计图补充完整;
(2)如果该校学生有1800人,请你估计该校喜欢“唱歌”这项宣传方式的学生约有多少人?
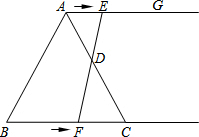 如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts. 如图,△ABC绕点C旋转后,顶点A旋转到了点D.
如图,△ABC绕点C旋转后,顶点A旋转到了点D.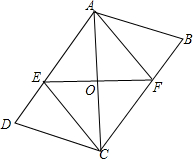 如图.四边形ABCD中,AB=CD,AD=BC,对角线AC的中点为O,过点O的直线分别交AD、BC于点E、F.
如图.四边形ABCD中,AB=CD,AD=BC,对角线AC的中点为O,过点O的直线分别交AD、BC于点E、F.