题目内容
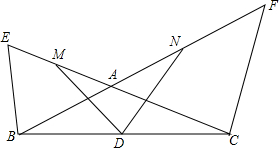 如图,BF、CE相交于点A,BE=BA,CA=CF,若D、M、N分别是BC,AE,AF的中点.
如图,BF、CE相交于点A,BE=BA,CA=CF,若D、M、N分别是BC,AE,AF的中点.(1)求证:DM=DN:
(2)连接MN,若BC=14cm.MN=5cm.求△DMN的周长.
考点:三角形中位线定理,全等三角形的判定与性质
专题:
分析:(1)分别连接BM、CN,由条件可得BM⊥EC,CN⊥BF,再结合直角三角形的性质可得DM=DN=
BC;
(2)由(1)可求得DM和DN,可求得△DMN的周长.
| 1 |
| 2 |
(2)由(1)可求得DM和DN,可求得△DMN的周长.
解答:(1)证明:如图,分别连接BM、CN,

∵BE=BA,M为AE中点,
∴BM⊥CE,
∴△BMC为直角三角形,且D为BC中点,
∴DM=
BC,
同理可得DN=
BC,
∴DM=DN;
(2)解:∵BC=14cm,
∴DM=DN=
BC=7cm,
又∵MN=5cm,
∴DM+DN+MN=7cm+7cm+5cm=19cm,
即△DMN的周长为19cm.

∵BE=BA,M为AE中点,
∴BM⊥CE,
∴△BMC为直角三角形,且D为BC中点,
∴DM=
| 1 |
| 2 |
同理可得DN=
| 1 |
| 2 |
∴DM=DN;
(2)解:∵BC=14cm,
∴DM=DN=
| 1 |
| 2 |
又∵MN=5cm,
∴DM+DN+MN=7cm+7cm+5cm=19cm,
即△DMN的周长为19cm.
点评:本题主要考查等腰三角形、直角三角形的性质,掌握等腰三角形底边上的中线、高和顶角的平分相互重合是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=
中自变量x的取值范围是( )
| 2x-1 |
A、x≥-
| ||
B、x≥
| ||
| C、x≤-2 | ||
| D、x≤2 |
函数y=
的自变量x的取值范围是( )
| x-4 |
| A、x≠4 | B、x>4 |
| C、x≥4 | D、x≤4 |
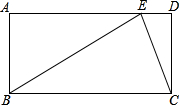 如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.
如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数. 如图,A,B,C三点在同一直线上,△ADC,△BEC是等边三角形,连接AE,BD.求证:
如图,A,B,C三点在同一直线上,△ADC,△BEC是等边三角形,连接AE,BD.求证: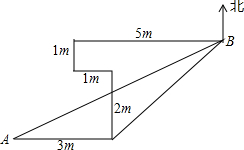 如图,小林在平坦的场地上从A点向东走了3m,再向北走了2m,再向西走了1m,又向北走了1m,最后向东走了5m,到达B点,求A、B之间的距离.
如图,小林在平坦的场地上从A点向东走了3m,再向北走了2m,再向西走了1m,又向北走了1m,最后向东走了5m,到达B点,求A、B之间的距离.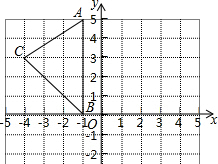 在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).