题目内容
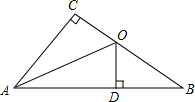 如图,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB于D,BD=4,OB=5,则BC=
如图,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB于D,BD=4,OB=5,则BC=考点:角平分线的性质
专题:
分析:先根据勾股定理求出OD的长,再由角平分线的性质可得出OC的长,进而得出结论.
解答:解:∵OD⊥AB于D,BD=4,OB=5,
∴OD=
=3.
∵∠C=90°,AO平分∠BAC,
∴OC=OD=3,
∴BC=OC+OB=3+5=8.
故答案为:8.
∴OD=
| 52-42 |
∵∠C=90°,AO平分∠BAC,
∴OC=OD=3,
∴BC=OC+OB=3+5=8.
故答案为:8.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、长方体、正方体都是棱柱 |
| B、六棱柱有六条棱、六个侧面 |
| C、三棱柱的侧面是三角形 |
| D、球体的三种视图均为同样的图形 |
A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上两点,则( )
| A、y1-y2>0 |
| B、y1-y2<0 |
| C、y1-y2=0 |
| D、y1,y2大小不确定 |
若若2×4n×8n=211,则n等于( )
| A、7 | B、4 | C、2 | D、6 |
 小明从正面观察如图所示的两个物体,其中所看到的图形是( )
小明从正面观察如图所示的两个物体,其中所看到的图形是( )A、 |
B、 |
C、 |
D、 |
下列各组数中,能构成直角三角形的是( )
| A、4,5,6 | ||
| B、6,8,11 | ||
C、1,1,
| ||
| D、5,12,2 |
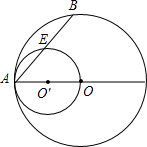 如图,⊙O的半径OA=2cm,以OA为直径的⊙O′交⊙O的弦AB于点E,若BE=
如图,⊙O的半径OA=2cm,以OA为直径的⊙O′交⊙O的弦AB于点E,若BE=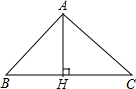 如图,△ABC中,AH是高,已知△ABC的面积为6,且BC2=2AH2+BH2+HC2,
如图,△ABC中,AH是高,已知△ABC的面积为6,且BC2=2AH2+BH2+HC2,