题目内容
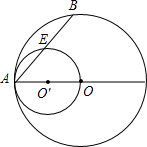 如图,⊙O的半径OA=2cm,以OA为直径的⊙O′交⊙O的弦AB于点E,若BE=
如图,⊙O的半径OA=2cm,以OA为直径的⊙O′交⊙O的弦AB于点E,若BE=| 2 |
考点:垂径定理,圆周角定理
专题:
分析:连接OE,根据圆周角定理可知∠AEO=90°,即OE⊥AB,根据垂径定理可知AE=BE=
cm,再由锐角三角函数的定义可得出∠BAO度数.
| 2 |
解答: 解:连接OE,
解:连接OE,
∵AO是⊙O′的直径,
∴∠AEO=90°,即OE⊥AB,
∴AE=BE=
cm,
∴AB=2AE=2
cm.
∵∠AEO=90°,
∴cos∠BAO=
=
,
∴∠BAO=45°.
故答案为:2
cm,45°.
 解:连接OE,
解:连接OE,∵AO是⊙O′的直径,
∴∠AEO=90°,即OE⊥AB,
∴AE=BE=
| 2 |
∴AB=2AE=2
| 2 |
∵∠AEO=90°,
∴cos∠BAO=
| AE |
| OA |
| ||
| 2 |
∴∠BAO=45°.
故答案为:2
| 2 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出圆周角是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法中不正确的是( )
A、
| ||
| B、有理数是正数和负数的统称 | ||
| C、-0.3是负分数 | ||
| D、0既不是正数,也不是负数 |
 如图,OC⊥AB于O,若∠AOD:∠COD=2:7,∠BOE:∠AOE=2:3,求∠DOE的度数.
如图,OC⊥AB于O,若∠AOD:∠COD=2:7,∠BOE:∠AOE=2:3,求∠DOE的度数. 如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=
如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB= 如图,在?ABCD中,E,F为BD上的点,BF=DE,那么四边形AECF是什么图形?试用两种方法证明.
如图,在?ABCD中,E,F为BD上的点,BF=DE,那么四边形AECF是什么图形?试用两种方法证明.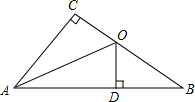 如图,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB于D,BD=4,OB=5,则BC=
如图,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB于D,BD=4,OB=5,则BC=