题目内容
A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上两点,则( )
| A、y1-y2>0 |
| B、y1-y2<0 |
| C、y1-y2=0 |
| D、y1,y2大小不确定 |
考点:一次函数图象上点的坐标特征
专题:计算题
分析:根据一次函数图象上点的坐标特征得到y1=-k+b,y2=3k+b,然后利用求差法比较大小.
解答:解:∵A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上两点,
∴y1=-k+b,y2=3k+b,
∴y1-y2=-k+b-3k-b=-4k,
而k<0,
∴y1-y2>0.
故选A.
∴y1=-k+b,y2=3k+b,
∴y1-y2=-k+b-3k-b=-4k,
而k<0,
∴y1-y2>0.
故选A.
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-
,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.
| b |
| k |

练习册系列答案
相关题目
两个有理数的积是正数,和是负数,那么这两个有理数( )
| A、同号,且均为负数 |
| B、异号,且正数的绝对值比负数的绝对值大 |
| C、同号,且均为正数 |
| D、异号,且负数的绝对值比正数的绝对值大 |
如图是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=
如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB= 二次函数y=-
二次函数y=-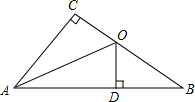 如图,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB于D,BD=4,OB=5,则BC=
如图,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB于D,BD=4,OB=5,则BC=