题目内容
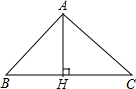 如图,△ABC中,AH是高,已知△ABC的面积为6,且BC2=2AH2+BH2+HC2,
如图,△ABC中,AH是高,已知△ABC的面积为6,且BC2=2AH2+BH2+HC2,(1)试判断△ABC形状,说明理由
(2)若HC2-BH2=7,求△ABC各边长.
考点:勾股定理的逆定理,勾股定理
专题:
分析:(1)先由三角形的高的定义得出∠AHB=∠AHC=90°,根据勾股定理得到AB2=AH2+BH2,AC2=AH2+HC2,那么AB2+AC2=2AH2+BH2+HC2,而BC2=2AH2+BH2+HC2,于是AB2+AC2=BC2,根据勾股定理的逆定理得到△ABC是直角三角形;
(2)由AC2=AH2+HC2,AB2=AH2+BH2,得出AC2-AB2=HC2-BH2=7,设AC=x,AB=y,则x2-y2=7 ①,由△ABC的面积为6,得出
xy=6,即xy=12 ②,①与②联立,解方程组求出AC=4,AB=3,利用勾股定理得到BC=
=5.
(2)由AC2=AH2+HC2,AB2=AH2+BH2,得出AC2-AB2=HC2-BH2=7,设AC=x,AB=y,则x2-y2=7 ①,由△ABC的面积为6,得出
| 1 |
| 2 |
| AC2+AB2 |
解答:解:(1)∵△ABC中,AH是高,
∴∠AHB=∠AHC=90°,
∴AB2=AH2+BH2,AC2=AH2+HC2,
∴AB2+AC2=AH2+BH2+AH2+HC2=2AH2+BH2+HC2,
∵BC2=2AH2+BH2+HC2,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
(2)∵AC2=AH2+HC2,AB2=AH2+BH2,
∴AC2-AB2=AH2+HC2-AH2-BH2=HC2-BH2=7,
设AC=x,AB=y,则x2-y2=7 ①,
∵△ABC的面积为6,
∴
xy=6,即xy=12 ②,
①与②联立,解得
,或
(不合题意舍去),
∴AC=4,AB=3,
∴BC=
=5.
∴∠AHB=∠AHC=90°,
∴AB2=AH2+BH2,AC2=AH2+HC2,
∴AB2+AC2=AH2+BH2+AH2+HC2=2AH2+BH2+HC2,
∵BC2=2AH2+BH2+HC2,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
(2)∵AC2=AH2+HC2,AB2=AH2+BH2,
∴AC2-AB2=AH2+HC2-AH2-BH2=HC2-BH2=7,
设AC=x,AB=y,则x2-y2=7 ①,
∵△ABC的面积为6,
∴
| 1 |
| 2 |
①与②联立,解得
|
|
∴AC=4,AB=3,
∴BC=
| AC2+AB2 |
点评:本题考查了勾股定理及其逆定理,三角形的面积,二元二次方程组的解法,三角形的高的定义,等式的性质,难度适中.正确求解二元二次方程组是解决第(2)题的关键.

练习册系列答案
相关题目
下列说法中不正确的是( )
A、
| ||
| B、有理数是正数和负数的统称 | ||
| C、-0.3是负分数 | ||
| D、0既不是正数,也不是负数 |
若点P(m,1)在第二象限内,则点Q(-m,0)在( )
| A、x轴正半轴上 |
| B、x轴负半轴上 |
| C、y轴正半轴上 |
| D、y轴负半轴上 |
下列由左到右的变形,属于因式分解的是( )
| A、m2-4=(m-2)(m+2) |
| B、(a+3)(a-3)=a2-9 |
| C、t2-16-6t=(t+4)(t-4)-6t |
| D、(m-2)(m-3)=(2-m)(3-m) |
若两个相似三角形的相似比为2:3,面积差是30,则它们的面积和为( )
| A、60 | B、78 |
| C、128 | D、150 |
 如图,已知BD、CE是△ABC的两条高,M、N分别是BC、DE的中点,请判断MN和DE的关系,并证明你的结论.
如图,已知BD、CE是△ABC的两条高,M、N分别是BC、DE的中点,请判断MN和DE的关系,并证明你的结论.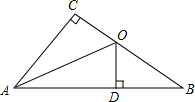 如图,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB于D,BD=4,OB=5,则BC=
如图,△ABC中,∠C=90°,AO平分∠BAC,OD⊥AB于D,BD=4,OB=5,则BC= 如图,∠1=88°,∠2=88°,∠3=50°,求∠4.
如图,∠1=88°,∠2=88°,∠3=50°,求∠4.