��Ŀ����
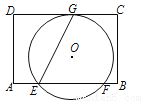
��ͼ��AB�ǡ�O��ֱ������C��D��Բ�ϣ����ı���AOCD��ƽ���ı��Σ�����D����O�����ߣ��ֱ�OA���ӳ�����OC���ӳ����ڵ�E��F������BF.
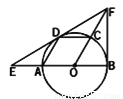
��1����֤��BF�ǡ�O�����ߣ�
��2����֪Բ�İ뾶Ϊ1����EF�ij�.
��1��֤������������2��EF=2. �����������������(1)����֤���ı���AOCD�����Σ��Ӷ��õ���AOD=��COD=60�㣬�ٸ������ߵ����ʵá�FDO=90�㣬����֤����FDO�ա�FBO�õ���ODF=��OBF=90�㣬Ȼ��������ߵ��ж��������ɵõ����ۣ�(2)����Rt��OBF�У�����60�ȵ����еĶ�����⣮ ���������(1)������OD����ͼ�����ı���AOCD��ƽ���ı��Σ���OA=OC...
��ϰ��ϵ�д�
 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д�
�����Ŀ


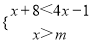 �Ľ⼯��x��3����m��ȡֵ��Χ��________��
�Ľ⼯��x��3����m��ȡֵ��Χ��________��
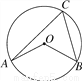
 AB����O������E�����CD����ֱ�������ڵ�G����GEBΪ��ǣ������AB����ֱ�߽�����һ��F����EG��EF��
AB����O������E�����CD����ֱ�������ڵ�G����GEBΪ��ǣ������AB����ֱ�߽�����һ��F����EG��EF��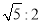 ������AD��BC���ڵ�ֱ�����O����ʱ��AB�ij��� .
������AD��BC���ڵ�ֱ�����O����ʱ��AB�ij��� .