题目内容
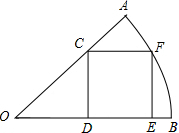如图，在半径为| 5 |
考点：勾股定理,正方形的性质
专题：
分析：连接OF，设正方形的边长为a．根据等腰直角三角形的性质，得OD=CD=a，在直角三角形OEF中，根据勾股定理列方程求得正方形的边长，再根据正方形的面积公式求解．
解答：
解：连接OF，设正方形的边长为a．
在Rt△OEF中，a2+（2a）2=（
）2，
解得a=1，
1×1=1．
答：正方形CDEF的面积是1．
故答案为：1．
解：连接OF，设正方形的边长为a．在Rt△OEF中，a2+（2a）2=（
| 5 |
解得a=1，
1×1=1．
答：正方形CDEF的面积是1．
故答案为：1．
点评：考查了勾股定理和正方形的性质，此题要能够发现等腰直角三角形的直角边等于正方形的边长，熟练运用勾股定理列方程求解，掌握正方形的面积公式．
练习册系列答案
轻松暑假总复习系列答案
相关题目
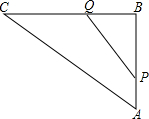如图，在Rt△ABC中，∠B=90°，AC=100cm，BC=80cm，点P从点A开始沿AB边向点B以1cm/s的速度运动，同时，另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动．
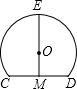如图，M是CD中点，EM⊥CD，若CD=6，EM=9，则C、E、D三点的所在圆的半径为
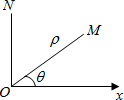在平面内取一个定点O，叫极点，引一条射线Ox，叫做极轴，再选定一个长度单位和角度的正方向（通常取逆时针方向）．对于平面内任何一点M，用ρ表示线段OM的长度，θ表示从Ox到OM的角度，ρ叫做点M的极径，θ叫做点M的极角，有序数对（ρ，θ）就叫点M的极坐标，若ON⊥OX，且点N到极点O的距离为4个单位长度，则点N的极坐标可表示为
如图，点C在直线MN上，AC⊥BC于点C，∠1=65°，则∠2=南海资源丰富，其面积约为350万平方千米，350万用科学记数法表示为（ ）
| A、0.35×108 |
| B、3.5×107 |
| C、3.5×106 |
| D、3.5×109 |