题目内容
等腰但不等边的三角形的角平分线、高线、的总条数是（ ）
A．3 B．5 C．7 D．9
C．
【解析】
试题分析：等腰但不等边的三角形底边上的角平分线、中线、高线三线重合成一条；腰上的三条线不重合，因而共有7条线．
故选C．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如图所示，已知l1∥l2，AB∥CD，CE⊥l2于点E，FG⊥l2于点G，则下列说法错误的是（ ）
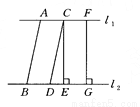
A. AB＝CD
B. CE＝FG
C. l1与l2之间的距离就是线段CE的长度
D. l1与l2之间的距离就是线段CD的长度
D
【解析】∵l1∥l2，AB∥CD，
∴四边形ABDC是平行四边形，
∴AB=CD，故选项A正确；
∵CE⊥l2于点E，FG⊥l2于点G，
∴CE∥FG，
∴四边形CEGF为平行四边形，
∴CE=FG，CF=EG，故选项B、C正确，
∵CD＞EC，AB=CD，
∴AB＞FG，故选项D错误.
故选D. 已知M=
，N=
，若a≠1，则M与N的大小关系为( )
A. M＞N B. M＜N C. M≤N D. M≥N
C
【解析】∵M＝，N＝，
∴M-N＝-
＝
＝
＝-≤0,
∴M≤N.
故选C. 如图，在△ABC 中，∠B 与∠C 的平分线交于点O， 过O 点作DE ∥BC，分别交AB、AC于D、E，若AB=5，AC=4，求△ADE 的周长.
9
【解析】试题分析：由在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，易证得△DOB与△EOC是等腰三角形，即DO=DB，EO=EC，继而可得△ADE的周长等于AB+AC，即可求得答案．
试题解析：
∵在△ABC中，∠B与∠C的平分线交于点O，
∴∠DBO=∠CBO，∠ECO=∠BCO，
∵DE∥BC，
∴∠DOB=∠CBO，∠EOC=∠BCO，... △ABC中，AB=AC，∠A=36°，BD平分∠ABC，则∠1 =_______度，此三角形有_______个等腰三角形．
72° 3
【解析】∵AB=AC，∠A=36°，
∴△ABC是等腰三角形，∠C=∠ABC=（180°?36°）=72°.
∵BD为∠ABC的平分线，
∴∠ABD=∠A=∠DBC=36°，
∴AD=BD，△ADB是等腰三角形，
∴∠1=180°-36°-72°=72°=∠C，
∴BC=BD，△CDB是等腰三角形.
图中共有3个等腰三角形． 如图，在矩形ABCD中，AB＜BC，AC，BD相交于点O，则图中等腰三角形的个数是
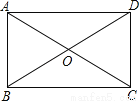
A．8 B．6 C．4 D．2
C
【解析】
试题分析：∵四边形ABCD是矩形，∴AO=BO=CO=DO。
∴△ABO，△BCO，△DCO，△ADO都是等腰三角形。
故选C。 等腰三角形的一个角是80°，则它的顶角的度数是（ ）
A. 80° B. 80°或20° C. 80°或50° D. 20°
B
【解析】试题分析：分80°角是顶角与底角两种情况讨论求解． ①80°角是顶角时，三角形的顶角为80°，
②80°角是底角时，顶角为180°﹣80°×2=20°， 综上所述，该等腰三角形顶角的度数为80°或20°． 如图，AB=AD，CB=CD，AC、BD相交于点O，则下列结论正确的是（ ）
A. OA=OC B. 点O到AB、CD的距离相等
C. ∠BDA=∠BDC D. 点O到CB、CD的距离相等
D
【解析】∵在△ADC和△ABC中，
，
∴△ADC≌△ABC，
∴∠DCA=∠BCA，
∴点O到CB、CD的距离相等.
故选D. （x+5y）2 等于（ ）
A. x2-5y 2 B. x2-10y+5y 2 C. x2+10xy+25y 2 D. x2-y+25y 2
C
【解析】根据完全平方公式可得：（x+5y）2=x2+10xy+25y 2 ，故选C.