题目内容
12. 已知一次函数y=kx+b的图象经过点A(-1,-5),且与正比例函数y=$\frac{1}{2}x$的图象相交于点B(2,a).
已知一次函数y=kx+b的图象经过点A(-1,-5),且与正比例函数y=$\frac{1}{2}x$的图象相交于点B(2,a).(1)求一次函数y=kx+b的表达式;
(2)在同一坐标系中,画出这两个函数的图象,并求这两条直线与y轴围成的三角形的面积;
(3)设一次函数y=kx+b的图象与y轴的交点是C,若点D与点O、B、C能构成平行四边形,请直接写出点D的坐标.
分析 (1)根据图象上的点满足函数解析式,可得B点坐标,根据待定系数法,可得一次函数的解析式;
(2)根据描点法,可得函数图象,根据三角形的面积公式,可得答案;
(3)分类讨论:OC∥BD,根据BD=OD,可得答案;OB∥CD,根据点平移的方向,平移的距离相同,可得答案.
解答 解:(1)正比例函数y=$\frac{1}{2}x$的图象经过点B(2,a),得
a=$\frac{1}{2}$×2=1,B(2,1).
一次函数y=kx+b的图象经过点A(-1,-5)与B(2,1),得
$\left\{\begin{array}{l}{-k+b=-5}\\{2k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=-3}\end{array}\right.$,
一次函数的解析式为y=2x-3;
(2)如图: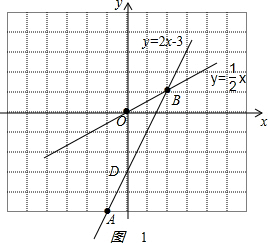 ,
,
S=$\frac{1}{2}$×3×2=3;
(3)如图2: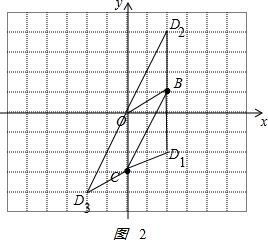 ,
,
当OC∥BD,BD=OC时,1-3=-2,即D1(2,-2);
当OC∥BD,BD=OC时,1+3=4,即D2(2,4);
当OB∥CD,OB=CD时,B点向下平移1个单位,再向左平移2个单位得到O点,
C点向下平移1个单位,再向左平移2个单位得到点D4(-2,-4).
综上所述:点D与点O、B、C能构成平行四边形,点D的坐标为(2,-2)(2,4),(-2,-4).
点评 本题考查了一次函数综合题,利用待定系数法是求函数解析式的关键,描点法画函数图象;利用平行四边形的判定:对边平行且相等的四边形是平行四边形,分类讨论是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 若a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是( )
若a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是( )
 若a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是( )
若a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是( )| A. | a+b<0 | B. | a+c<0 | C. | a-b>0 | D. | -b+c>0 |
7.在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )
| A. | ∠A=40°,∠B=50 | B. | ∠A=40°,∠B=60° | C. | ∠A=40°,∠B=70 | D. | ∠A=40°,∠B=80° |
5.下列命题是真命题的是( )
| A. | 直角三角形中两个锐角互补 | B. | 相等的角是对顶角 | ||
| C. | 同旁内角互补,两直线平行 | D. | 若|a|=|b|,则a=b |
 如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点
如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点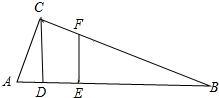 如图,已知在△ABC中,∠ACB=90°,CD是斜边AB上的高,在AB上截取AE=AC,过点E作EF∥CD,交BC于点F,DE=1厘米,求点E到BC的距离.
如图,已知在△ABC中,∠ACB=90°,CD是斜边AB上的高,在AB上截取AE=AC,过点E作EF∥CD,交BC于点F,DE=1厘米,求点E到BC的距离. 如图,线段AB=4,点O是线段AB上一点,C,D分 别是线段OA,OB的中点.
如图,线段AB=4,点O是线段AB上一点,C,D分 别是线段OA,OB的中点.