题目内容
2. 如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点
如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点求证:四边形EGFH是菱形.
分析 由已知条件得出GF是△ADC的中位线,GE是△ABC的中位线,EH是△ABD的中位线,由三角形中位线定理得出GF∥EH,GF=EH,得出四边形EGFH是平行四边形,再证出GE=EH,即可得出结论.
解答 证明:∵点E、F、G、H分别是AB、CD、AC、BD的中点,
∴GF是△ADC的中位线,GE是△ABC的中位线,EH是△ABD的中位线,
∴GF∥AD,GF=$\frac{1}{2}$AD,GE=$\frac{1}{2}$BC,EH∥AD,EH=$\frac{1}{2}$AD,
∴GF∥EH,GF=EH,
∴四边形EGFH是平行四边形,
又∵AD=BC,
∴GE=EH,
∴四边形EGFH是菱形.
点评 本题考查了三角形中位线定理、平行四边形的判定、菱形的判定方法;熟练掌握菱形的判定方法,由三角形中位线定理得出线段之间的关系是解决问题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
12.下列方程是一元二次方程的是( )
| A. | x2+3y-5=0 | B. | $\frac{1}{x}$-2x2+1=0 | ||
| C. | ax2+bx+c=0(其中a、b、c为常数) | D. | $\sqrt{3}$x2+4x-5=0 |
13.2008年5月12日,四川汶川发生8.3级大地震,据统计这次地震直接经济损失大约600 000 000 000元,这个数据用科学记数法表示为( )
| A. | 0.6×1012元 | B. | 6×1012元 | C. | 6×1011元 | D. | 60×1010元 |
10.an=3,am=2,a2n-3m=( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{9}{8}$ | D. | $\frac{11}{8}$ |
14.下列各组数据不能作为直角三角形的三边长的是( )
| A. | a=3 b=4 c=5 | B. | a=6 b=8 c=10 | C. | a=5 b=12 c=13 | D. | a=13 b=16 c=18 |
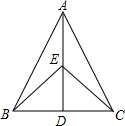 已知:如图,AB=AC,AD⊥BC于D,点E在AD上,图中共有3对全等三角形.
已知:如图,AB=AC,AD⊥BC于D,点E在AD上,图中共有3对全等三角形. 已知一次函数y=kx+b的图象经过点A(-1,-5),且与正比例函数y=$\frac{1}{2}x$的图象相交于点B(2,a).
已知一次函数y=kx+b的图象经过点A(-1,-5),且与正比例函数y=$\frac{1}{2}x$的图象相交于点B(2,a).