题目内容
15．
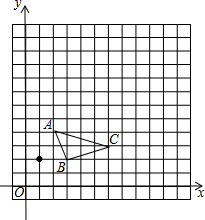如图，在13x13的网格图中，已知△ABC的顶点坐标分别为A（2，4）、B（3，2）、C（6，3）．（1）以点M（1，2）为位似中心，在第一象限把△ABC按相似比2：1放大，得△A'B'C'，画出△ABC的位似图形；
（2）写出△A'B'C'的各顶点坐标．
分析 （1）延长MA到A′使MA′=2MA，则点A′为点A的对应点，同样方法得到点B、C的对应点B′、C′，从而得到△A'B'C'；
（2）利用第一象限点的坐标特征写出△A'B'C'的各顶点坐标．
解答 解：（1）如图，△A′B′C′为所作；
（2）A′（3，6），B′（5，2），C′（11，4）．
点评 本题考查了作图-位似变换：先确定位似中心；再分别连接并延长位似中心和能代表原图的关键点；接着根据位似比，确定能代表所作的位似图形的关键点；然后顺次连接上述各点，得到放大或缩小的图形．
练习册系列答案
全优点练单元计划系列答案
相关题目
如图，四边形ABCD中，∠ABC的平分线与外角∠DCE的平分线相交于点P，若∠A=140°，∠D=120°，则∠BPC=40度．
10．
如图所示，Rt△ABO中，∠AOB=90°，点A在第一象限，点B在第四象限，且AO：BO=1：$\sqrt{2}$，若点A（x0，y0）的坐标（x0，y0）满足y0=$\frac{1}{{y}_{0}}$，则点B（x，y）的坐标x，y所满足的关系式为（ ）
如图所示，Rt△ABO中，∠AOB=90°，点A在第一象限，点B在第四象限，且AO：BO=1：$\sqrt{2}$，若点A（x0，y0）的坐标（x0，y0）满足y0=$\frac{1}{{y}_{0}}$，则点B（x，y）的坐标x，y所满足的关系式为（ ）| A． | y=$\frac{-2}{x}$ | B． | y=$\frac{-\sqrt{2}}{x}$ | C． | y=$\frac{-1}{x}$ | D． | y=$\frac{1}{x}$ |
如图，五边形ABCDE中，AB∥CD，∠1，∠2，∠3是五边形的外角，则∠1+∠2+∠3等于180°．
如图，小明同学将一个圆锥和一个三棱柱组成组合图形，观察其三视图，其俯视图是（ ）
