题目内容
10. 如图所示,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第四象限,且AO:BO=1:$\sqrt{2}$,若点A(x0,y0)的坐标(x0,y0)满足y0=$\frac{1}{{y}_{0}}$,则点B(x,y)的坐标x,y所满足的关系式为( )
如图所示,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第四象限,且AO:BO=1:$\sqrt{2}$,若点A(x0,y0)的坐标(x0,y0)满足y0=$\frac{1}{{y}_{0}}$,则点B(x,y)的坐标x,y所满足的关系式为( )| A. | y=$\frac{-2}{x}$ | B. | y=$\frac{-\sqrt{2}}{x}$ | C. | y=$\frac{-1}{x}$ | D. | y=$\frac{1}{x}$ |
分析 设点B坐标为(x,y),分别过点A、B作AC,BD分别垂直y轴于点C、D,由相似三角形的判定定理得出△AOC∽△OBD,再由相似三角形的性质得出△OBD的面积,进而根据三角形面积公式可得出结论.
解答 解:设点B坐标为(x,y),分别过点A、B作AC,BD分别垂直y轴于点C、D,
∵∠ACO=∠BDO=90°,
∠AOC+∠BOD=90°,
∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
∴△AOC∽△OBD,
∴$\frac{{S}_{△AOC}}{{S}_{△BOD}}=(\frac{OA}{0B})^{2}=(\frac{1}{\sqrt{2}})^{2}=\frac{1}{2}$,
∵点A(x0,y0)的坐标x0,y0满足y0=$\frac{1}{{y}_{0}}$,
∴S△AOC=$\frac{1}{2}$,
∴S△BOD=1,
而点B坐标为(x,y),
∴$\frac{1}{2}$x•(-y)=1,
∴y=-$\frac{2}{x}$.
故选A
点评 此题考查了反比例函数图象上点的坐标特点,此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
7.解二元一次方程组$\left\{\begin{array}{l}{3x+4y=2(1)}\\{2x-y=5(2)}\end{array}\right.$,最恰当的变形是( )
| A. | 由①得x=$\frac{2-4y}{3}$ | B. | 由②得y=2x-5 | C. | 由①得x=$\frac{2-3y}{4}$ | D. | 由②得x=$\frac{y+5}{2}$ |
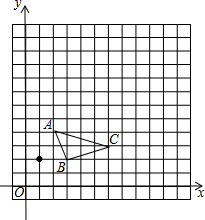 如图,在13x13的网格图中,已知△ABC的顶点坐标分别为A(2,4)、B(3,2)、C(6,3).
如图,在13x13的网格图中,已知△ABC的顶点坐标分别为A(2,4)、B(3,2)、C(6,3). 如图,已知?ABCD的对角线AC与 BD相交于点O,过点O作EF⊥AC,与边AD、BC 分别交于点 E、F.求证:四边形AFCE是菱形.
如图,已知?ABCD的对角线AC与 BD相交于点O,过点O作EF⊥AC,与边AD、BC 分别交于点 E、F.求证:四边形AFCE是菱形.