题目内容
20. 如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3是五边形的外角,则∠1+∠2+∠3等于180°.
如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3是五边形的外角,则∠1+∠2+∠3等于180°.
分析 根据两直线平行,同旁内角互补求出∠B+∠C=180°,从而得到以点B、点C为顶点的五边形的两个外角的度数之和等于180°,再根据多边形的外角和定理列式计算即可得解.
解答  解:∵AB∥CD,
解:∵AB∥CD,
∴∠B+∠C=180°,
∴∠4+∠5=180°,
根据多边形的外角和定理,∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°-180°=180°.
故答案为:180°.
点评 本题考查了平行线的性质,多边形的外角和定理,是基础题,理清求解思路是解题的关键.

练习册系列答案
相关题目
5.下列各数中,为无理数的是( )
| A. | $\root{3}{-8}$ | B. | $\frac{5}{2}$ | C. | $\sqrt{36}$ | D. | $\root{3}{2}$ |
12.已知正方形ABCD中,E是BC上一点,如果DE=2,CE=1,那么正方形ABCD的面积为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | 4 | D. | 5 |
 已知如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
已知如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
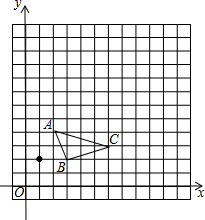 如图,在13x13的网格图中,已知△ABC的顶点坐标分别为A(2,4)、B(3,2)、C(6,3).
如图,在13x13的网格图中,已知△ABC的顶点坐标分别为A(2,4)、B(3,2)、C(6,3). 如图,在△ABC中,∠C=90°,点D是AB边上的一点,DE⊥AB于D,交AC于M,且ED=AC,过点E作EF∥BC分别交AB、AC于点F、N.
如图,在△ABC中,∠C=90°,点D是AB边上的一点,DE⊥AB于D,交AC于M,且ED=AC,过点E作EF∥BC分别交AB、AC于点F、N.