题目内容
12. 如图,四边形ABCD中,∠ABC的平分线与外角∠DCE的平分线相交于点P,若∠A=140°,∠D=120°,则∠BPC=40度.
如图,四边形ABCD中,∠ABC的平分线与外角∠DCE的平分线相交于点P,若∠A=140°,∠D=120°,则∠BPC=40度.
分析 利用四边形内角和是360°可以求得∠ABC+∠BCD=160°然后由角平分线的性质,邻补角的定义求得∠PBC+∠BCP的度数,所以根据△BCP的内角和定理求得∠P的度数即可.
解答 解:如图,∵∠A=140°,∠D=120°,
∴∠ABC+∠BCD=100°.
又∵∠ABC的平分线与外角∠DCE的平分线相交于点P,
∴∠PBC+∠BCP=$\frac{1}{2}$∠ABC+∠BCD+$\frac{1}{2}$(180°-∠BCD)=90°+$\frac{1}{2}$(∠ABC+∠BCD)=140°,
∴∠BPC=180°-(∠PBC+∠BCP)=40°.
故答案是:40.
点评 本题考查了三角形内角和定理、多边形的内角与外角.熟知“四边形的内角和是360°”是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
2.地理老师介绍到:长江比黄河长836米,黄河长度的6倍比长江长度的5倍多1284千米,小东根据地理教师的介绍,设长江长为x千米,黄河长为y千米,那么下面列出的方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=836}\\{5x-6y=1284}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=836}\\{6x-5y=1284}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=836}\\{6x-5y=1284}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=836}\\{6y-5x=1284}\end{array}\right.$ |
3.一个长方形的长为8,宽为4,分别以两组对边中点的连线为坐标轴建立平面直角坐标系,下面那个点不在长方形上( )
| A. | (4,-2) | B. | (-2,4) | C. | (4,2) | D. | (0,-2) |
7.解二元一次方程组$\left\{\begin{array}{l}{3x+4y=2(1)}\\{2x-y=5(2)}\end{array}\right.$,最恰当的变形是( )
| A. | 由①得x=$\frac{2-4y}{3}$ | B. | 由②得y=2x-5 | C. | 由①得x=$\frac{2-3y}{4}$ | D. | 由②得x=$\frac{y+5}{2}$ |
 已知如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
已知如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线. 如图,已知正方形ABCD的边长为1,点E在边DC上,AE平分∠DAC,EF⊥AC,点F为垂足,那么FC=$\sqrt{2}$-1.
如图,已知正方形ABCD的边长为1,点E在边DC上,AE平分∠DAC,EF⊥AC,点F为垂足,那么FC=$\sqrt{2}$-1.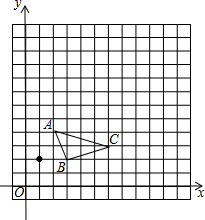 如图,在13x13的网格图中,已知△ABC的顶点坐标分别为A(2,4)、B(3,2)、C(6,3).
如图,在13x13的网格图中,已知△ABC的顶点坐标分别为A(2,4)、B(3,2)、C(6,3).