题目内容
4.为了提高足球基本功,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.(1)请用树状图列举出三次传球的所有可能情况;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
分析 (1)根据题意画出树状图即可;
(2)根据(1)的树形图,利用概率公式列式进行计算即可得解,分别求出球回到甲脚下的概率和传到乙脚下的概率,比较大小即可.
解答 解:(1)根据题意画出树状图如下: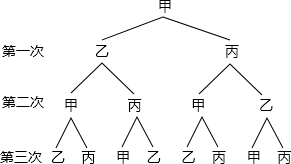
由树形图可知三次传球有8种等可能结果;
(2)由(1)可知三次传球后,球回到甲脚下的概率=$\frac{2}{8}$=$\frac{1}{4}$;传到乙脚下的概率=$\frac{3}{8}$,
所以球回到乙脚下的概率大.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.

练习册系列答案
相关题目
19.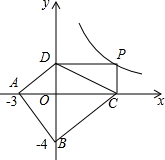 如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )
如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )
 如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )
如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )| A. | 12 | B. | 13 | C. | 24 | D. | 26 |
16.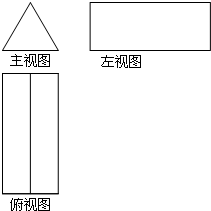 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )
 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )| A. | 正三棱柱 | B. | 正三棱锥 | C. | 圆锥 | D. | 圆柱 |
5.在-$\frac{5}{3}$,-$\sqrt{2}$,-$\sqrt{3}$,-$\frac{π}{2}$四个数中,最大的数是( )
| A. | -$\frac{5}{3}$ | B. | -$\sqrt{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{π}{2}$ |
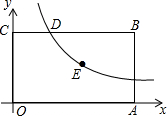 如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形的对称中心E,且与边BC交于点D,则点CD的长为1.
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形的对称中心E,且与边BC交于点D,则点CD的长为1. 如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为4或$\frac{9}{4}$cm.
如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为4或$\frac{9}{4}$cm.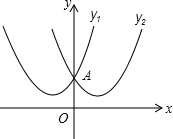 定义感知:我们把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”,其“共点”为点A.
定义感知:我们把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”,其“共点”为点A.