题目内容
19．
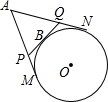如图，A为⊙O外一点，AM、AN分别切⊙O于M、N点，PQ切⊙O于B，且交AM、AN分别于P、Q点．若AM=10，则△APQ的周长为20．
分析 根据切线长定理证明AM=AN、PB=PM，QB=QN，根据三角形的周长公式计算得到答案．
解答 解：∵AM、AN分别切⊙O于M、N点，
∴AM=AN=10，
∵PQ切⊙O于B，
∴PB=PM，QB=QN，
△APQ的周长为AP+PQ+AQ=AP+PB+BQ+AD
=AP+PM+QN+AQ
=AM+AN
=20，
故答案为：20．
点评 本题考查的是切线长定理的应用，掌握从圆外一点引圆的两条切线，它们的切线长相等是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
10．在某次体育测试中，九年级一班女同学的一分钟仰卧起坐成绩（单位：个）如下表：
这此测试成绩的中位数和众数分别为（ ）
| 成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人数 | 1 | 1 | 4 | 2 | 5 | 2 |
| A． | 47，49 | B． | 47，50 | C． | 48，49 | D． | 48，50 |
14．下列各式中属于最简二次根式的是（ ）
| A． | $\sqrt{{x}^{2}+1}$ | B． | $\sqrt{{x}^{2}{y}^{3}}$ | C． | $\sqrt{12}$ | D． | $\sqrt{\frac{1}{2}}$ |
4．
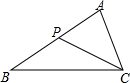已知：如图，△ABC中，P为AB上的一点，在下列四个条件中：
①∠ACP=∠B；②∠APC=∠ACB；③AB•CP=AP•CB；④AC•AC=AP•AB，
能使△APC和△ACB相似的条件有（ ）
已知：如图，△ABC中，P为AB上的一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AB•CP=AP•CB；④AC•AC=AP•AB，
能使△APC和△ACB相似的条件有（ ）
| A． | ①②④ | B． | ①③④ | C． | ②③④ | D． | ①②③ |
8．若x＞y，则下列式子中错误的是（ ）
| A． | x-3＞y-3 | B． | 3-x＞3-y | C． | 2x＞2y | D． | -$\frac{x}{4}$$＜-\frac{y}{4}$ |