题目内容
4.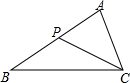 已知:如图,△ABC中,P为AB上的一点,在下列四个条件中:
已知:如图,△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AB•CP=AP•CB;④AC•AC=AP•AB,
能使△APC和△ACB相似的条件有( )
| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
分析 △APC和△ACB有公共角∠A,则根据有两组角对应相等的两个三角形相似可对(1)、(2)进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对(3)、(4)进行判断.
解答 解:∵∠PAC=∠CAB,
∴当∠ACP=∠B时,△ACP∽△APC,所以(1)正确;
当∠APC=∠ACB时,△ACP∽△APC,所以(2)正确;
当$\frac{AP}{AC}=\frac{AC}{AB}$,即AC2=AP•AB时,△ACP∽△APC,所以(3)正确,(4)错误.
故选D.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.充分利用△APC和△ACB的公共角.

练习册系列答案
相关题目
14.如果x-$\frac{1}{x}$=3,则${x^2}+\frac{1}{x^2}$的值为( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
15.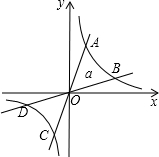 如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
 如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 任意四边形 |
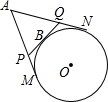 如图,A为⊙O外一点,AM、AN分别切⊙O于M、N点,PQ切⊙O于B,且交AM、AN分别于P、Q点.若AM=10,则△APQ的周长为20.
如图,A为⊙O外一点,AM、AN分别切⊙O于M、N点,PQ切⊙O于B,且交AM、AN分别于P、Q点.若AM=10,则△APQ的周长为20.