题目内容
16.观察下列式子,并完成后面的问题:13+23=$\frac{1}{4}×{2^2}×{3^2}$
13+23+33=$\frac{1}{4}×{3^2}×{4^2}$
13+23+33+43=$\frac{1}{4}×{4^2}×{5^2}$
…
(1)13+23+33+43+…+n3=$\frac{1}{4}$×n2×(n+1)2;
(2)(2n)3=2n×2n×2n=2×2×2n•n•n=23n3=8n3.你能利用上述关系计算23+43+63+83+…+203=24200;
(3)得用(1)、(2)得到结论,73+93+…+193等于多少吗?并写出你是怎样得到的?
分析 (1)观察不难发现,从1开始的连续自然数的立方和等于自然数的个数的平方乘比个数大1的数的平方,再除以4;
(2)将原式变形为(2×1)3+(2×2)3+(2×3)3+(2×4)3+…+(2×10)3=8×(13+23+33+43+…+103),再套用(1)中公式计算可得;
(3)由(1)得13+23+33+43+…+203=$\frac{1}{4}$×202×212=44100,由(2)得23+43+63+83+…+203=8×$\frac{1}{4}$×102×112=24200,两式相减从而得出13+33+53+73+…+193,再减去13+33+53即可得答案.
解答 解:(1)∵13=$\frac{1}{4}$×12×22,
13+23=$\frac{1}{4}$×22×32,
13+23+33=$\frac{1}{4}$×32×42,
∴13+23+33+…+(n-1)3+n3=$\frac{1}{4}$×n2×(n+1)2;
故答案为:$\frac{1}{4}$×n2×(n+1)2;
(2)原式=(2×1)3+(2×2)3+(2×3)3+(2×4)3+…+(2×10)3
=8×(13+23+33+43+…+103)
=8×$\frac{1}{4}$×102×112
=24200,
故答案为:24200;
(3)由(1)知13+23+33+43+…+203=$\frac{1}{4}$×202×212=44100,
由(2)知,23+43+63+83+…+203=8×$\frac{1}{4}$×102×112=24200,
∴13+33+53+73+…+193=44100-24200=19900,
又∵13+33+53=1+27+125=153,
∴73+93+…+193=19747.
点评 本题主要考查数字的变化规律,根据题意得出数字的规律是从1开始的连续自然数的立方和等于自然数的个数的平方乘比个数大1的数的平方,再除以4是解题的关键.

| A. | 2(a-b)=2a-2b | B. | x2-2x+1=x(x-2)+1 | ||
| C. | (m+1)(m-1)=m2-1 | D. | 3a(a-1)+(1-a)=(3a-1)(a-1) |
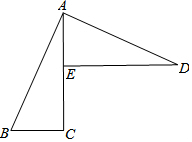 已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.求证:AB=AD.
已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.求证:AB=AD. 如图,在梯形ABCD中,AB∥DC,AC、BD相交于点O,如果S三角形AOB=16cm2,S三角形COD=9cm2,则S三角形DOC:S三角形COB=3:4.
如图,在梯形ABCD中,AB∥DC,AC、BD相交于点O,如果S三角形AOB=16cm2,S三角形COD=9cm2,则S三角形DOC:S三角形COB=3:4.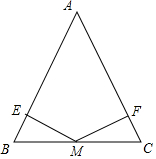 已知AB=AC,∠BME=∠CMF,点M是BC的中点.求证:EM=FM.
已知AB=AC,∠BME=∠CMF,点M是BC的中点.求证:EM=FM.