题目内容
10.若α,β为直角三角形的两个锐角,若cosα=$\frac{5}{9}$,求sinβ的值.分析 根据互余两角三角函数的关系进行解答.
解答 解:∵α,β为直角三角形的两个锐角,
∴sinβ=cos(90°-β)=cosα=$\frac{5}{9}$.
点评 本题考查的是互余两角三角函数的关系,在直角三角形中,∠A+∠B=90°时,正余弦之间的关系为:①一个角的正弦值等于这个角的余角的余弦值,即sinA=(90°-∠A);②一个角的余弦值等于这个角的余角的正弦值,即cosA=sin(90°-∠A);也可以理解成若∠A+∠B=90°,那么sinA=cosB或sinB=cosA.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
8.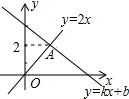 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点A,则不等式
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点A,则不等式
0<2x<kx+b的解集是( )
 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点A,则不等式
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点A,则不等式0<2x<kx+b的解集是( )
| A. | x<1 | B. | x<0或x>1 | C. | 0<x<1 | D. | x>1 |
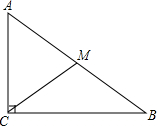 如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,CM是中线,以2.5cm为半径画⊙C,试判断A、B、M三点与⊙C的位置关系.
如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,CM是中线,以2.5cm为半径画⊙C,试判断A、B、M三点与⊙C的位置关系. 如图,△ABC的中线BE,CF相交于点G,证明:BG=2GE,CG=2GF.
如图,△ABC的中线BE,CF相交于点G,证明:BG=2GE,CG=2GF.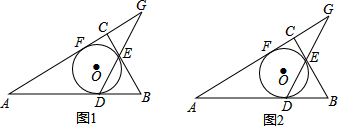
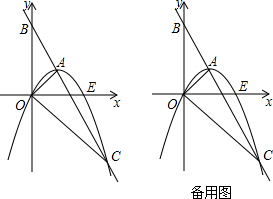
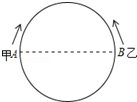 如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=$\frac{1}{2}{t^2}+\frac{3}{2}$t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=$\frac{1}{2}{t^2}+\frac{3}{2}$t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.