题目内容
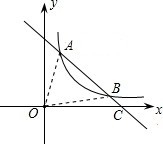 如图,双曲线y=
如图,双曲线y=| k |
| x |
(1)求反比例函数和一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)根据图象直接写出在第一象限内一次函数的值大于反比例函数的值时,x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)将A坐标代入反比例解析式中求出k的值,确定出反比例解析式,将B纵坐标代入反比例解析式中求出横坐标,确定出B的坐标,将A与B坐标代入一次函数解析式中求出m与n的值,即可确定出一次函数解析式;
(2)过A、B分别作x轴的垂线,垂足分别为D、E,三角形OAB面积=三角形OAC面积-三角形BOC面积,求出即可;
(3)找出图象上一次函数在反比例函数上方时x的范围即可.
(2)过A、B分别作x轴的垂线,垂足分别为D、E,三角形OAB面积=三角形OAC面积-三角形BOC面积,求出即可;
(3)找出图象上一次函数在反比例函数上方时x的范围即可.
解答: 解:(1)将A(1,5)代入反比例解析式得:k=5,
解:(1)将A(1,5)代入反比例解析式得:k=5,
∴反比例解析式为y=
,
将y=1代入y=
中得:x=5,即B(5,1),
将A与B代入一次函数解析式得:
,
解得:
,
则一次函数解析式为y=-x+6;
(2)对于一次函数y=-x+6,令y=0,求出x=6,即C(6,0),
∴OC=6,
又AD=5,BE=1,
则S△AOB=S△AOC-S△BOC=
×6×5-
×6×1=12;
(3)根据图象得:当1<x<5时,一次函数的值大于反比例函数的值.
 解:(1)将A(1,5)代入反比例解析式得:k=5,
解:(1)将A(1,5)代入反比例解析式得:k=5,∴反比例解析式为y=
| 5 |
| x |
将y=1代入y=
| 5 |
| x |
将A与B代入一次函数解析式得:
|
解得:
|
则一次函数解析式为y=-x+6;
(2)对于一次函数y=-x+6,令y=0,求出x=6,即C(6,0),
∴OC=6,
又AD=5,BE=1,
则S△AOB=S△AOC-S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据图象得:当1<x<5时,一次函数的值大于反比例函数的值.
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,一次函数与坐标轴的交点,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
节约能源,从我做起,为响应号召,小李决定将家里的4只白炽灯全部换成节能灯,商场有功率为4w和5w两种型号的节能灯若干可供选择,则买到的节能灯都为同一型号的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是由四个相同立方体组成的立体图形的主视图和左视图,则原立体图形可能是( )


| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
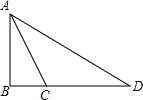 如图,在△ABC中.∠B=90°,∠BAC=30°.AB=9cm,D是BC延长线上一点.且AC=DC.则
如图,在△ABC中.∠B=90°,∠BAC=30°.AB=9cm,D是BC延长线上一点.且AC=DC.则 某拱桥的横截面呈抛物线形,桥下水面宽为AB(单位:米).以水面宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系.抛物线解析式为y=-x2+4
某拱桥的横截面呈抛物线形,桥下水面宽为AB(单位:米).以水面宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系.抛物线解析式为y=-x2+4
 车厘子就是英语单词cherries(樱桃)的音译,车厘子的含铁量特别高,位于各种水果之首,常食车厘子可补充体内对铁元素的需求,促进血红蛋白再生,既可防治缺铁性贫血.又可增强体质,健脑益智,车厘子营养丰富,具有调中益气,健脾和胃,祛风湿,“令人面孔好颜色”之功效,对食欲不振,消化不良,风湿身痛等等均有益处.2011年1月份至6月份重庆市某商场车厘子销售价格y(元)与月份x(1≤x≤6且x为整数)之间的函数关系式如下表:
车厘子就是英语单词cherries(樱桃)的音译,车厘子的含铁量特别高,位于各种水果之首,常食车厘子可补充体内对铁元素的需求,促进血红蛋白再生,既可防治缺铁性贫血.又可增强体质,健脑益智,车厘子营养丰富,具有调中益气,健脾和胃,祛风湿,“令人面孔好颜色”之功效,对食欲不振,消化不良,风湿身痛等等均有益处.2011年1月份至6月份重庆市某商场车厘子销售价格y(元)与月份x(1≤x≤6且x为整数)之间的函数关系式如下表: