题目内容
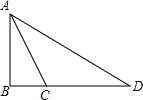 如图,在△ABC中.∠B=90°,∠BAC=30°.AB=9cm,D是BC延长线上一点.且AC=DC.则
如图,在△ABC中.∠B=90°,∠BAC=30°.AB=9cm,D是BC延长线上一点.且AC=DC.则AD=
考点:含30度角的直角三角形
专题:计算题
分析:由AC=CD,利用等边对等角得到一对角相等,在直角三角形ABC中,由两锐角互余求出∠ACB的度数,由外角性质求出∠D为30°,利用30°角所对的直角边等于斜边的一半即可求出AD的长.
解答:解:∵AC=CD,
∴∠CAD=∠D,
在Rt△ABC中,∠B=90°,∠BAC=30°,
∴∠ACB=60°,
∵∠ACB为△ACD的外角,
∴∠CAD=∠D=30°,
∴AD=2AB=18cm.
故答案为:18
∴∠CAD=∠D,
在Rt△ABC中,∠B=90°,∠BAC=30°,
∴∠ACB=60°,
∵∠ACB为△ACD的外角,
∴∠CAD=∠D=30°,
∴AD=2AB=18cm.
故答案为:18
点评:此题考查了含30度直角三角形的性质,外角性质,以及等腰三角形的性质,熟练掌握性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若x=-2是关于x的方程2x+3m+1=0的解,则m的值为( )
A、
| ||
B、-
| ||
| C、-1 | ||
| D、1 |
下列分式变形错误的是( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
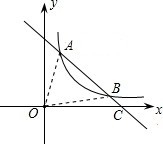 如图,双曲线
如图,双曲线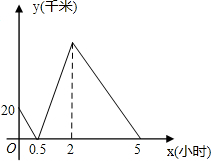 在一条笔直的航道上有A、B、C三个港口,一艘轮船从A港出发,匀速航行到C港后返回到B港,轮船离B港的距离y(千米),与航行时间x(小时)之间的函数关系如图所示,若航行过程中水流速度和轮船的静水速度保持不变,则水流速度为
在一条笔直的航道上有A、B、C三个港口,一艘轮船从A港出发,匀速航行到C港后返回到B港,轮船离B港的距离y(千米),与航行时间x(小时)之间的函数关系如图所示,若航行过程中水流速度和轮船的静水速度保持不变,则水流速度为