题目内容
19. 某公司推出的高效环保洗条用品,年初上市后,经历了从亏损到盈利的过程,下面的二次函数的图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系).
某公司推出的高效环保洗条用品,年初上市后,经历了从亏损到盈利的过程,下面的二次函数的图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系).根据图象提供的信息,解答系列问题:
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系
(2)求第7个月公司所获利润为多少万元?
分析 (1)通过构建函数模型解答销售利润的问题,应根据图象以及题目中所给的信息来列出y与x之间的函数关系式;
(2)分别把x=6,x=7,代入函数解析=$\frac{1}{2}$x2-2x,再把总利润相减就可得出.
解答 解:(1)由图象可知其顶点坐标为(2,-2),
故可设其函数关系式为:y=a(x-2)2-2.
∵所求函数关系式的图象过(0,0),
于是得:
a(0-2)2-2=0,
解得a=$\frac{1}{2}$.
∴所求函数关系式为:y=$\frac{1}{2}$(x-2)2-2,即y=$\frac{1}{2}$x2-2x.
答:累积利润y与时间x之间的函数关系式为:y=$\frac{1}{2}$x2-2x;
(2)把x=6代入关系式,
得y=$\frac{1}{2}$×62-2×6=6,
把x=7代入关系式,
得y=$\frac{1}{2}$×72-2×7=10.5,
10.5-6=4.5,
答:第7个月公司所获利是4.5万元.
点评 此题主要考查了二次函数的性质在实际生活中的应用,我们首先要吃透题意,确定变量,建立函数模型,尤其是对本题图象中所给的信息是解决问题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
9.某市今年预计建成34个地下调蓄设施,蓄水能力达到140000立方米,将140000用科学记数法表示应为( )
| A. | 14×104 | B. | 1.4×105 | C. | 1.4×106 | D. | 0.14×106 |
11.要反映自贡市一周内每天的最高气温的变化情况,宜采用( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
9.下列运算正确的是( )
| A. | -a(a-b)=-a2-ab | B. | (2ab)2÷a2b=4ab | C. | 2ab•3a=6a2b | D. | (a-1)(1-a)=a2-1 |
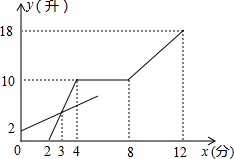 现有甲、乙两个容器,分别装有进水管和出水管,且两容器各自的进水速度不变、出水速度不变.甲、乙两容器的进水管和出水管均关闭.现先打开乙容器的进水管,2分钟后再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管,直到12分钟时,同时关闭两容器的进、出水管,打开和关闭水管的时间忽略不计.甲、乙两容器中各自的水量y(升)与乙容器注水时间x(分钟)之间的函数关系的图象如图所示.
现有甲、乙两个容器,分别装有进水管和出水管,且两容器各自的进水速度不变、出水速度不变.甲、乙两容器的进水管和出水管均关闭.现先打开乙容器的进水管,2分钟后再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管,直到12分钟时,同时关闭两容器的进、出水管,打开和关闭水管的时间忽略不计.甲、乙两容器中各自的水量y(升)与乙容器注水时间x(分钟)之间的函数关系的图象如图所示.