题目内容
1．
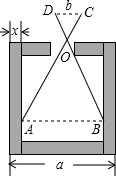如图，已知零件的外径为a，现用一个交叉卡钳（两条尺长AC和BD相等）测量零件的内孔直径AB，如果OA：OC=OB：OD=n．且量得CD=b．求AB以及零件厚度x．
分析 根据两边对应成比例夹角相等，两三角形相似判断出△ABO和△CDO相似，再根据相似三角形对应边成比例求出AB，然后根据厚度x=$\frac{1}{2}$（a-AB）计算即可得解．
解答 解：∵OA：OC=OB：OD，∠AOB=∠COD（对顶角相等），
∴△ABO∽△CDO，
∴AB：CD=OA：OC=n，
∴AB=nCD=bn，
∴厚度x=$\frac{1}{2}$（a-AB）=$\frac{1}{2}$（a-bn）．
点评 本题考查了相似三角形的应用，判断出三角形相似并根据相似三角形对应边成比例求出AB的长是解题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
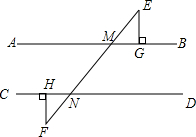如图，直线EF和AB，CD分别相交于点M，N，EG⊥AB，FH⊥CD，垂足分别为G，H，且∠BME=53°，∠F=37°，试利用“三角形内角和等于180°”说明直线AB∥CD，EG∥FH．
如图，点O在直线AB上，OC⊥OD，若∠AOD=36°，求∠COB的度数．