题目内容
2.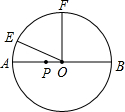 已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )
已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )| A. | 5cm | B. | 5$\sqrt{2}$cm | C. | 5$\sqrt{3}$cm | D. | 10cm |
分析 作点F′与点F关于AB对称.连接EF′,EF′交AB与点P,连接PF、EF.由轴对称的性质可知PE+FP=EP+PF′=EF′,然后再Rt△EFF′中求得∠EF′F=30°
,由特殊锐角三角函数值可求得EF′的长度.
解答 解:如图所示,作点F′与点F关于AB对称.连接EF′,EF′交AB与点P,连接PF、EF.
∵点F′与点F关于AB对称,
∴PF′=PF.
∴PE+FP=EP+PF′=EF′.
∵FF′是圆O的直径,
∴∠FEF′=90°.
∵∠AOE=30°,
∴∠EOF=60°.
∴∠EF′F=30°.
∴$\frac{EF′}{FF′}=\frac{\sqrt{3}}{2}$,即$\frac{EF′}{10}=\frac{\sqrt{3}}{2}$.
∴EF′=5$\sqrt{3}$.
∴PE+PF=5$\sqrt{3}$.
故选:C.
点评 本题主要考查的是翻折的性质、轴对称--路径最短、圆周角定理、特殊锐角三角函数值,求得∠EF′F=30°是解题的关键.

练习册系列答案
相关题目
12.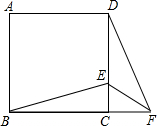 如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )
 如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )| A. | 25° | B. | 30° | C. | 45° | D. | 60° |
7.下面哪个点在函数y=-2x+3的图象上( )
| A. | (-5,-7) | B. | (0.5,2) | C. | (3,0) | D. | (1,-5) |
 如图,Rt△ABC中,∠B=90°,画出P点为旋转中心,按顺时针方向旋转180°后的△A′B′C′.
如图,Rt△ABC中,∠B=90°,画出P点为旋转中心,按顺时针方向旋转180°后的△A′B′C′.