题目内容
2.先化简,再求值:($\frac{{a}^{2}-4}{{a}^{2}-4a+4}$-$\frac{2}{2-a}$)÷$\frac{2}{{a}^{2}-2a}$,其中a是方程x2+3x-10=0的根.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{a+2+2}{a-2}$•$\frac{a(a-2)}{2}$
=$\frac{a+4}{a-2}$•$\frac{a(a-2)}{2}$
=$\frac{{{a^2}+4a}}{2}$,
∵a是方程x2+3x-10=0的根,
∴a1=-5,a2=2(舍去).
当a=-5时,原式=$\frac{{(-5)}^{2}+4×(-5)}{2}$=2.5.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
12.$\sqrt{\frac{1}{16}}$的平方根是( )
| A. | ±$\frac{1}{2}$ | B. | ±$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
13.下列运算正确的是( )
| A. | 2$\sqrt{2}×\sqrt{2}=4$ | B. | 2a3•a4=2a7 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
12.已知直线y=kx+b,若k+b<0,kb>0,那么该直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
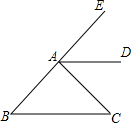 如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.
如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.