题目内容
19.在平面直角坐标系中,已知抛物线y=ax2+bx+c经过点A(-3,0),B(1,0),C(0,3)三点.(1)求抛物线的解析式.
(2)在抛物线上是否存在点P,使tan∠PBA=$\frac{1}{3}$?若存在,求点P坐标及△PAB的面积.
(3)将△COB沿x轴负方向平移1.5个单位至△FGH处,求△FGH与△AOC的重叠面积.
(4)若点D、E分别是抛物线的对称轴l上的两动点,且纵坐标分别为n,n+6,求CE+DB的最小值及此时D、E的坐标.
分析 (1)设交点式y=a(x+3)(x-1),然后把C点坐标代入求出a即可得到抛物线解析式;
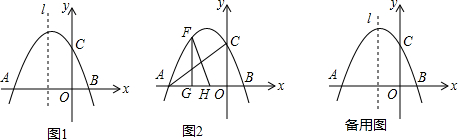
(2)作PH⊥x轴于H,如图1,设P(t,-t2-2t+3),分类讨论:利用tan∠PBA=$\frac{PH}{BH}$=$\frac{1}{3}$得到$\frac{-{t}^{2}-2t+3}{1-t}$=$\frac{1}{3}$,或$\frac{-(-{t}^{2}-2t+3)}{1-t}$=$\frac{1}{3}$,然后分别解方程求出t得到P点坐标,再利用三角形面积公式计算对应的△PAB的面积;
(3)FG、FH分别交AC于N、M,如图2,利用待定系数法求出直线BC的解析式为y=-3x+3,再利用直线平移的规律得到直线FH的解析式为y=-3x-$\frac{3}{2}$,利用点平移的规律得到H(-$\frac{1}{2}$,0),G(-$\frac{3}{2}$,0),接着通过解方程组$\left\{\begin{array}{l}{y=-3x-\frac{3}{2}}\\{y=x+3}\end{array}\right.$得M(-$\frac{9}{8}$,$\frac{15}{8}$),然后根据三角形面积公式,利用△FGH与△AOC的重叠面积=S△MAO-S△ANG进行计算即可;
(4)把C点沿y轴向下平移6个单位得到G(0,-3),连结AG交抛物线的对称轴(直线x=-1)于D,连结DB,易得四边形CEDG为平行四边形,则DG=CE,由于DB+CE=DA+DG=AG,根据两点之间线段最短可判断此时DB+CE最小,根据勾股定理可计算出最小值,接着求出直线AG的解析式,然后确定D点和E点坐标.
解答 解:(1)设抛物线解析式为y=a(x+3)(x-1),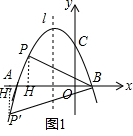
把C(0,3)代入得a•3•(-1)=3,解得a=-1,
所以抛物线的解析式为y=-(x+3)(x-1),即y=-x2-2x+3;
(2)存在.
作PH⊥x轴于H,如图1,tan∠PBA=$\frac{PH}{BH}$=$\frac{1}{3}$,
设P(t,-t2-2t+3),
当点P在x轴上方时,$\frac{-{t}^{2}-2t+3}{1-t}$=$\frac{1}{3}$,
整理得3t2+5t-8=0,解得t1=1(舍去),t2=-$\frac{8}{3}$,
此时P点坐标为(-$\frac{8}{3}$,$\frac{11}{9}$),S△PAB=$\frac{1}{2}$•(1+3)•$\frac{11}{9}$=$\frac{22}{9}$;
当点P在x轴下方时,$\frac{-(-{t}^{2}-2t+3)}{1-t}$=$\frac{1}{3}$,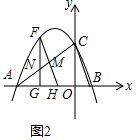
整理得3t2+7t-10=0,解得t1=1(舍去),t2=-$\frac{10}{3}$,
此时P点坐标为(-$\frac{10}{3}$,-$\frac{13}{9}$),S△PAB=$\frac{1}{2}$•(1+3)•$\frac{13}{9}$=$\frac{26}{9}$;
综上所述,P点坐标为(-$\frac{8}{3}$,$\frac{11}{9}$),S△PAB=$\frac{22}{9}$;P点坐标为(-$\frac{10}{3}$,-$\frac{13}{9}$),S△PAB=$\frac{26}{9}$;
(3)FG、FH分别交AC于N、M,如图2,
设直线BC的解析式为y=mx+n,
把C(0,3),B(1,0)代入得$\left\{\begin{array}{l}{n=3}\\{m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-3}\\{n=3}\end{array}\right.$,
所以直线BC的解析式为y=-3x+3,
把直线y=-3x+3向左平移$\frac{3}{2}$个单位得到直线FH的解析式为y=-3(x+$\frac{3}{2}$)+3=-3x-$\frac{3}{2}$,点B平移到H(-$\frac{1}{2}$,0),点O平移得到G(-$\frac{3}{2}$,0)
易得直线AC的解析式为y=x+3,△OAC为等腰直角三角形,则△ANG为等腰直角三角形,
所以NG=AG=3-$\frac{3}{2}$=$\frac{3}{2}$,解方程组$\left\{\begin{array}{l}{y=-3x-\frac{3}{2}}\\{y=x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{9}{8}}\\{y=\frac{15}{8}}\end{array}\right.$,则M(-$\frac{9}{8}$,$\frac{15}{8}$),
所以△FGH与△AOC的重叠面积=S△MAO-S△ANG=$\frac{1}{2}$×(-$\frac{1}{2}$+3)×$\frac{15}{8}$-$\frac{1}{2}$×$\frac{3}{2}$×$\frac{3}{2}$=$\frac{39}{32}$;
(4)把C点沿y轴向下平移6个单位得到G(0,-3),连结AG交抛物线的对称轴(直线x=-1)于D,连结DB,如图3,
则DB=DA,DE=CG,
所以四边形CEDG为平行四边形,则DG=CE,
所以DB+CE=DA+DG=AG,此时DB+CE最小,最小值为$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
设直线AG的解析式为y=px+q,
把A(-3,0),G(0,-3)代入得$\left\{\begin{array}{l}{-3p+q=0}\\{q=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{p=-1}\\{q=-3}\end{array}\right.$,
所以直线AG的解析式为y=-x-3,
当x=-1时,y=-x-3=-2,则D(-1,-2),E(-1,4).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式;记住三角形面积公式,理解坐标与图形性质;能利用两点之间线段最短解决最短路径问题.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | 周长相等的两个三角形全等 | |
| B. | 关于某条直线对称的两个三角形全等 | |
| C. | 顶角相等的两个等腰三角形全等 | |
| D. | 两边和一角对应相等的两个三角形全等 |
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 以上都不对 |