题目内容
已知反比例函数y=-
,当x取-1,2,-6,
-3中某一个数时,能使y的值大于零的概率是( )
| 15 |
| x |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:概率公式,函数值
专题:
分析:由反比例函数y=-
,当x取-1,2,-6,
,-3,可得y的值分别为:15,-
,
,-
,5;然后直接利用概率公式求解即可求得答案.
| 15 |
| x |
| 2 |
| 3 |
| 15 |
| 2 |
| 5 |
| 2 |
| 45 |
| 2 |
解答:解:∵反比例函数y=-
,当x取-1,2,-6,
,-3,可得y的值分别为:15,-
,
,-
,5;
∴共有5种等可能的结果,能使y的值大于零的有3种情况,
∴能使y的值大于零的概率是:
.
故选C.
| 15 |
| x |
| 2 |
| 3 |
| 15 |
| 2 |
| 5 |
| 2 |
| 45 |
| 2 |
∴共有5种等可能的结果,能使y的值大于零的有3种情况,
∴能使y的值大于零的概率是:
| 3 |
| 5 |
故选C.
点评:此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
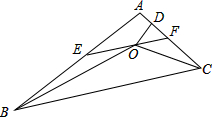 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;
②∠BOC=90°+
| 1 |
| 2 |
③EF不能成为△ABC的中位线;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
| A、①②③ | B、①②④ |
| C、②③④ | D、①③④ |
已知m<2,点A(x1,y1)、B(x2,y2)在双曲线y=
上,如果x1<x2,那么y1与y2的大小关系是( )
| 2-m |
| x |
| A、y1=y2 |
| B、y1>y2 |
| C、y1<y2 |
| D、无法确定 |
说明命题“如果a,b,c是△ABC的三边,那么长为a-1,b-1,c-1的三条线段能构成三角形”是假命题的反例可以是( )
| A、a=2,b=2,c=3 |
| B、a=2,b=2,c=2 |
| C、a=3,b=3,c=4 |
| D、a=3,b=4,c=5 |
下列四个实数中,最小的数是( )
| A、0.01 | ||
B、-
| ||
| C、-0.1 | ||
| D、-2 |
在
,2,4,-2这四个数中,互为相反数的是( )
| 1 |
| 2 |
A、
| ||
| B、2与-2 | ||
C、-2与
| ||
| D、-2与4 |
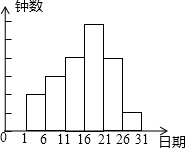 在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题: