题目内容
19.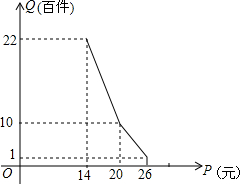 某小型残疾人企业经营某种消费品专卖店,这种消费品的进价为每件14元;该店月销量Q(百件)与销售价格P(元)的关系如图;
某小型残疾人企业经营某种消费品专卖店,这种消费品的进价为每件14元;该店月销量Q(百件)与销售价格P(元)的关系如图;(1)求该店月销量Q(百件)与销售价格P(元)的函数关系式;
(2)当商品的价格每件多少元时,月利润最大?并求出最大值.
分析 (1)根据函数图象是分段函数,于是应求14≤P≤20与20<P≤26两部分的函数的解析式,由图象上的点代入Q=aP+b,求出即可;
(2)根据月销量与利润的积,求出月销量Q(百件)与销售价格P(元)的函数关系式,求出最值即可.
解答 解:(1)设月销量Q(百件)与销售价格P(元)的函数关系式为:Q=aP+b,
当14≤P≤20时,由图象得$\left\{\begin{array}{l}{14a+b=22}\\{20a+b=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=50}\end{array}\right.$,
∴Q=-2P+50,
同理求得20<P≤26时,Q=-$\frac{3}{2}$x+40,
∴Q=$\left\{\begin{array}{l}{-2P+50(14≤P≤20)}\\{-\frac{3}{2}P+40(20<P≤26)}\end{array}\right.$;
(2)由(1)知,当14≤P≤20时,y=100(P-14)(-2P+50)=-200P2+7800P-70000,
当P=-$\frac{7800}{-2×2}$=19.5时,y最大=112550,
当20<P≤26时,y=100(P-14)(-$\frac{3}{2}$P+40)=-150P2+6100P-5600,
当P=$\frac{6100}{2×(-150)}$=$\frac{61}{3}$时,y最大=$\frac{202850}{3}$<112550,
综上所述:当商品的价格每件19.5元时,月利润最大,为112550元.
点评 本题考查了二次函数的应用,待定系数法求函数的解析式,二次函数的最大值,正确的列出函数的解析式是解题的关键.

| A. | 22.5° | B. | 45° | C. | 67.5° | D. | 135° |
| A. | 8、15、16 | B. | 6、3$\sqrt{2}$、2$\sqrt{3}$ | C. | 3$\sqrt{2}$、4$\sqrt{2}$、5$\sqrt{2}$ | D. | 6、2$\sqrt{10}$、2$\sqrt{6}$ |
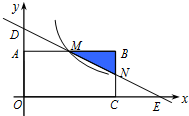 如图,在直角坐标系中,长方形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图,在直角坐标系中,长方形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.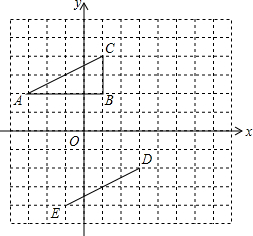 在平面直角坐标系中,△ABC的顶点坐标是A(-3,2),B(1,2),C(1,4).线段DE的端点坐标是D(3,-2),E(-1,-4).
在平面直角坐标系中,△ABC的顶点坐标是A(-3,2),B(1,2),C(1,4).线段DE的端点坐标是D(3,-2),E(-1,-4).