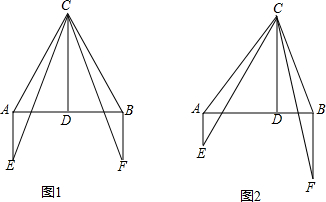
题目内容
如图，P为线段AB上一点，AD与BC交于E，∠CPD=∠A=∠B，BC交PD于F，AD交PC于G，则图中
相似三角形有（ ）
| A．1对 | B．2对 | C．3对 | D．4对 |
C
解析试题分析：先根据条件证明△PCF∽△BCP，利用相似三角形的性质：对应角相等，再证明△APD∽△PGD，进而证明△APG∽△BFP
再证明时注意图形中隐含的相等的角．
解：∵∠CPD=∠B，∠C=∠C，
∴△PCF∽△BCP．
∵∠CPD=∠A，∠D=∠D，
∴△APD∽△PGD．
∵∠CPD=∠A=∠B，
∴∠APG=∠BFP，
∴△APG∽△BFP．
故选C．
考点：相似三角形的判定．
点评：本题考查相似三角形的判定．识别两三角形相似，除了要掌握定义外，还要注意正确找出两三角形的对应边、对应角．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
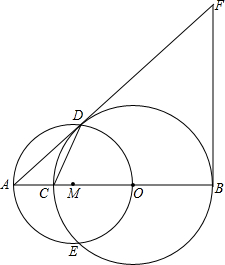如图，C为线段AB上一点，以BC为直径作⊙O，再以AO为直径作⊙M交⊙O于D、B作AB的垂线交AD的延长线于F，连接CD．若AC=2，且AC与AD的长是关于x的方程x2-
如图，C为线段AB上的一点，△ACM、△CBN都是等边三角形，若AC=3，BC=2，则△MCD与△BND的面积比为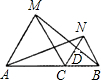
如图，C为线段AB上的一点，△ACM、△CBN都是等边三角形，BM与CN交于D点．若AC=3，BC=2，则CD=
7、如图，P为线段AB上一点，AD与BC交干E，∠CPD=∠A=∠B，BC交PD于E，AD交PC于G，则图中