题目内容
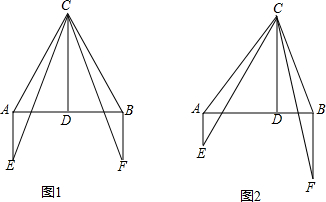
如图，C为线段AB上的一点，△ACM、△CBN都是等边三角形，若AC=3，BC=2，则△MCD与△BND的面积比为分析：利用△ACM、△CBN都是等边三角形，则也是相似三角形，相似比是3：2，再证得△MCD∽△BND，则面积比可求．
解答：解：∵△ACM、△CBN都是等边三角形，
∴△ACM∽△CBN，
∴CM：BN=AC：BC=3：2；
∵△ACM、△CBN都是等边三角形，
∴∠MCA=∠NDB=∠BND=60°，
∴∠MCN=60°=∠BND，
∴∠CMD=∠NBD（三角形内角和定理）
∴△MCD∽△BND
∴△MCD与△BND的面积比为（
）2=（
）2=
．
∴△ACM∽△CBN，
∴CM：BN=AC：BC=3：2；
∵△ACM、△CBN都是等边三角形，
∴∠MCA=∠NDB=∠BND=60°，
∴∠MCN=60°=∠BND，
∴∠CMD=∠NBD（三角形内角和定理）
∴△MCD∽△BND
∴△MCD与△BND的面积比为（
| BN |
| CM |
| 3 |
| 2 |
| 9 |
| 4 |
点评：本题考查对相似三角形的判定及性质的理解．相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
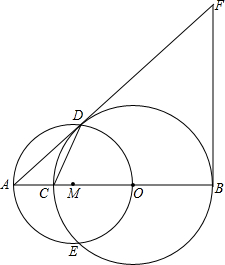如图，C为线段AB上一点，以BC为直径作⊙O，再以AO为直径作⊙M交⊙O于D、B作AB的垂线交AD的延长线于F，连接CD．若AC=2，且AC与AD的长是关于x的方程x2-
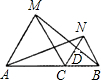如图，C为线段AB上的一点，△ACM、△CBN都是等边三角形，BM与CN交于D点．若AC=3，BC=2，则CD=
7、如图，P为线段AB上一点，AD与BC交干E，∠CPD=∠A=∠B，BC交PD于E，AD交PC于G，则图中